Essay 2: Hearts From an Ellipse
Ashley Jones
There are many geometric shapes, circles, squares, etc, that catch our attention throughout mathematical explorations. One such geometric shape that we do not think about coming across too often in our mathematical explorations is the heart. With mathematics we can create perfectly symmetrical hearts of all different sizes. There are many mathematical explorations that will allow us to construct a heart shape, for this example I focused on the use of ellipses. An ellipse algebraically, is the locus of points whose sum of distance from two fixed points, focii, remains constant (Coolmath.com). Check out this website for a 'user' friendly explanation and animation of an ellipse: http://www.coolmath.com/algebra/25-conic-sections/02_ellipses-intro.htm.
Using Geometer's Sketchpad, we can first begin by creating our own ellipse. This will help us to understand the mathematical concept of ellipses as well as gain more practice using the tools of GSP. I have attached a Geometer's Sketchpad file that will allow you to use the ellipse tool I created (AJones: Ellipse). To see the steps I took in order to perform this construction select 'Show Script View' when performing the construction using the tool. This will give you a text box that contains the necessary steps to construct your own ellipse. Below is the link to the GSP file containing the ellipse tool. For this tool, you need to select the tool, click two points on the screen so that they are not intersecting, and a third point within the circle. Careful not to drag the final point outside of the circle. This will create a hyperbola, which is closely related to an ellipse. However, we will not be discussing it in this essay.
When working with ellipses, we generally are introduced to the equation: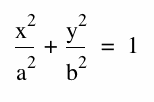 
. For this equation we define the parameters a and b as the lengths of the minor and major axis. These two lengths, allow us to find the appropriate locus around the foci to construct our ellipse. In our examples used, the lengths of both axis are equal to 1. The general equation for an ellipse used below is: 
. By changing the sign of the yx term in our equation, we allow ourselves to reflect the original ellipse and thus construct a heart using ellipses. In fact, there can be two hearts found in this graph below. For the first heart, the top is located in the first and second quadrants. The second heart is found in the third and fourth quadrants. Both of the hearts are constructed using parts of the original equation and the reflected equation. Below is the illustration of the two equations and the hearts formed.
Equations of reflected Ellipse: 
and 
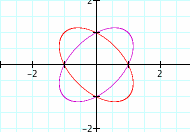
Varying the first coefficient between the values of 1 and 10: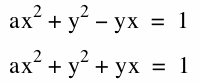 
By varying the first coefficient we can see that the graph changes in the horizontal direction. When the value of the parameter is equivalent to 0 the graphs of the equations become the same. As the value of the parameter increases, the domain of the graphs become a larger interval.
Varying the second coefficient between the values of 1 and 10: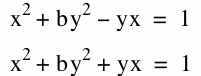 
By varying the second coefficient, b, we can see that the graph changes in the vertical direction. When the value of the parameter is equivalent to 0 the graphs of the equations become the same. As the value of the parameter increases, the range of the graphs become a larger interval.
Varying the third coefficient between the values of -2 and 2: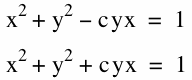 
By varying the third coefficient, c, we can see that the graph changes into a hyperbola. When the value of the parameter is equivalent to 0 the graphs of the equations become the same (circle shape). As the value of the parameter increases, the domain and range of the graphs both become larger intervals.
Varying the equality value between the values of 1 and 10: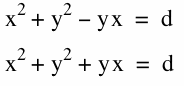 
By varying the equality value, d, we can see that the graph remains in the same shape where we can clearly determine the two hearts. When the value of the parameter is equivalent to 0 the graphs of the equations disappear. As the value of the parameter increases, both the domain and range of the graphs become larger intervals.
When we re-write the equation in such a way, we are able to construct a heart. Instead of having two equations to represent adding and subtracting the yx term, we now have one term where we take the absolute value of x: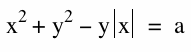 
Again, when we vary the equality value, a, we can see that the graph remains in the shape of a heart. By using the absolute value of the parameter x, we are able to transform the graph by reflecting it across the x-axis to obtain the negative values. When the value of the parameter is equivalent to 0 the graph of the equation disappears. As the value of the parameter increases, both the domain and range of the graphs become larger intervals. As the heart grows and shrinks we are able to illustrate mathmatically the image of a beating heart.
If we look at the image created by decreasing the above parameter, a, we will see different sized hearts encompassed in one another.
