Roxanne Kerry

For my eighth write up, I chose to further my exploration of the orthocenter of a triangle and various related properties. To begin with, I constructed the orthocenter of a triangle and the circumcircle of it. Then, I found where the lines containing the altitudes of the triangle intersect with the circumcircle, and marked them as well. I want to determine the relationship among these various points and if they have anything in common. See construction below:

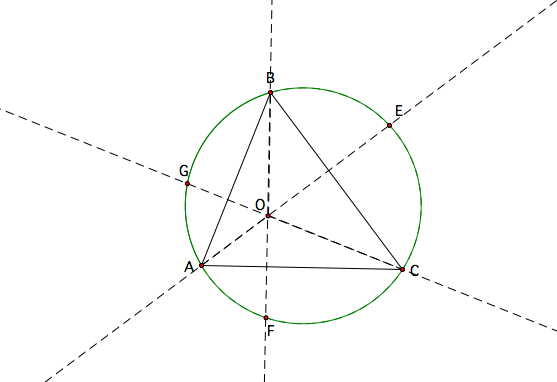
First, I will explore the relationship between the lengths of the segments from the vertices to the orthocenter and from the vertices to the opposing points on the circumcircle. The measures calculated using the Geometer's Sketchpad are as follows:

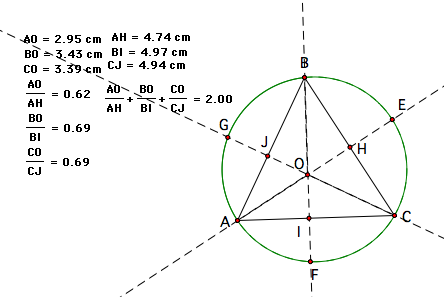
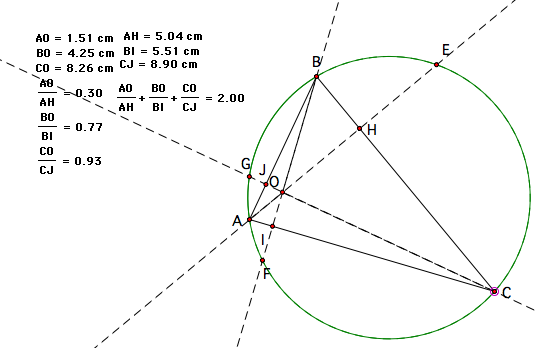
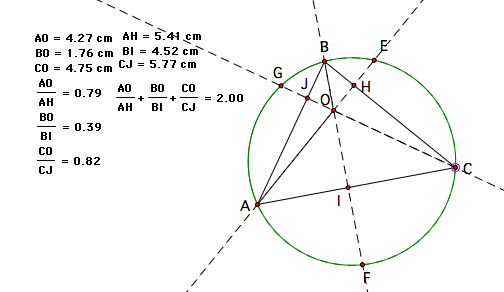
As you can see from these three sample snapshots, we come to quite the interesting conclusion: that adding these ratios of the length from the vertex to the orthocenter over the length of the vertex to the opposing side of the triangle will always equal 2! Now in these examples, the triangle is always acute. Will this work when the triangle is right or obtuse?

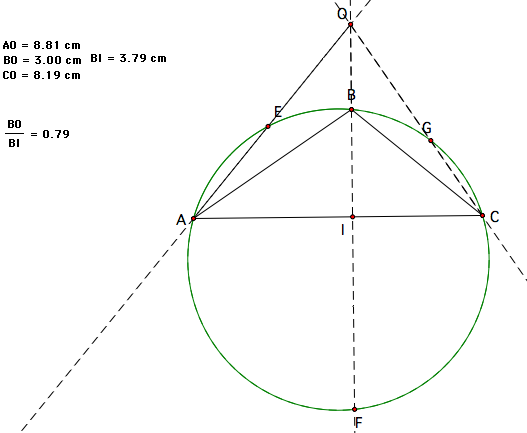
The answer is no, and if you think about it, it makes sense, because the lines from each vertex to the orthocenter no longer cross the opposing sides of the triangle. So this interesting triangle property only works when the triangle is acute.

Upon further analysis, I made another conclusion that the ratios of the other pieces of the altitudes to each altitude has just as interesting of a property, which is, the sum of these three ratios is equal to 1! See below:

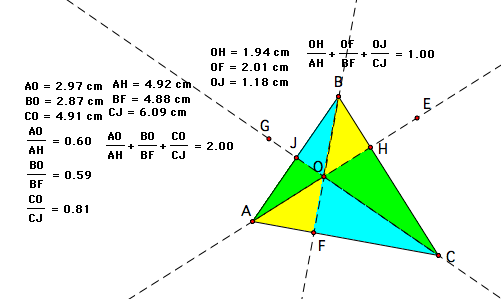
Moving the vertices of the triangle as with the above exploration, we see that the sum of the ratios stays the same as long as the triangle remains acute.

So, my hypothesis is that first, that adding these ratios of the length from the vertex to the orthocenter over the length of altitude will always equal 2, and second, that adding these ratios of the length from the orthocenter to the opposing side of each vertex over the length of the altitude will always equal to 1. But how in the word could we prove this?

There are a few things we know about altitudes and these triangles. The first and most basic conclusion we can make is that the length of the altitude is equal to the length from the vertex to the orthocenter plus the length from the orthocenter to the opposing side. We know this by construction, AO + OH = AH, BO+OF = BF, and CO+OJ=CJ.

We also can conclude that the triangles of the same color in my construction are in fact similar, by looking at their angles. Since CJ is perpendicular to AB, and AH is perpendicular to BC, and BF is perpendicular to CA, we can conclude that angle AOF is congruent to BOE, FOC is congruent to JOB, and that COH is congruent to AOJ. Also, we know that these triangles are right triangles by construction, since the altitudes are perpendicular to the opposing sides, therefore the third angle of the corresponding triangles are similar and thus the triangles of the same color are similar.

We can write our first conclusion in the form of proportions to get

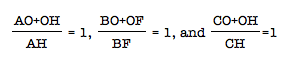
Conclusively, we can rewrite these fractions to get

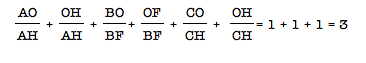
But wait, what if we add our two conclusions made earlier?

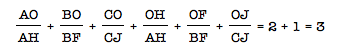
These tell you the same thing! So in conclusion, the two formulas found before hold valid due simply to properties of the altitudes and relationships among the vertices, edges of the triangle, and the orthocenter! This even makes more sense why these formulas hold true only given an acute triangle, because then the orthocenter is the intersection of the three altitudes of the triangle, which no longer goes through each of the sides, so no relationships can be made!