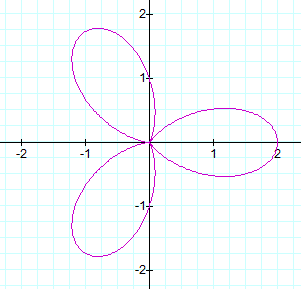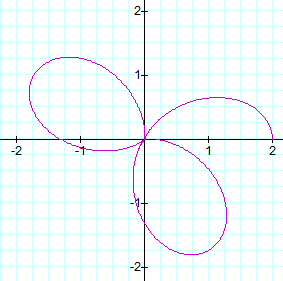Assignment 11

Polar equations

Let’s investigate the following equation:

and it’s graph:

This shape is called a n-leaf rose and this shape is maintained as long as a and b are equal.

When a and b increase and decrease together, the n-leaf becomes larger and smaller respectively.

When a and b become negative, the n-leaf reflects about the y-axis and becomes larger as a and b continue to decrease.

Here are the graphs of the equation at various values of a and b.

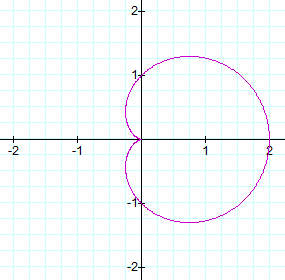
When a = 2 and b = 2:

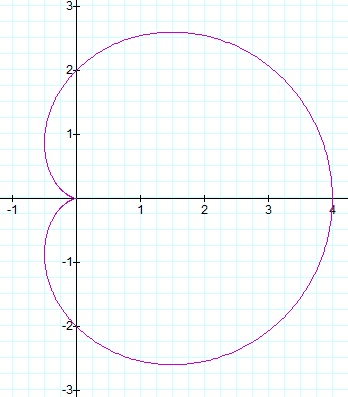
When a = -2 and b = -2:

What happens if we now change the value of k?

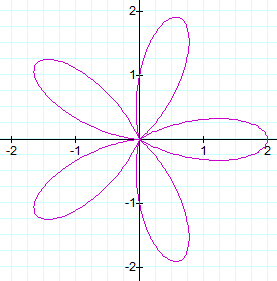
When k = 0, the shape of the graph is that of a circle When k is an integer, the n-leaf rose has a number of leaves equal to the absolute value of k with one of the leaves on and symmetrical to the positive x-axis (I call this the base leaf).

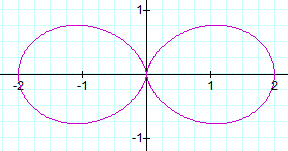
When k = 2

When k = 3

When k = 5

What k is a non integer, the graph is a shape that is in transition from the graph of the greatest integer less than k to the least integer greater than k.

The graph below represents the equation when k = 2.4.

As you can see the graph is in transition between k = 2 and k = 3. It has more than two leaves, and is in the process of gaining it’s third leaf.

What happens when cosine is replaced with sine?

The above properties are the same except for the orientation of the shapes.

When k = 0 the graph is of the same circle, but when k=1 the 1-leaf rose is now symmetrical with the y-axis.

When k = 2, the base leaf is symmetrical with the line y=x.

Further increases in the integer value of k result in the base leaf being symmetrical with a line that approaches the x-axis.