---

William Plummer - Assignment #2

Examine the following formula:

and its graph when a = 1 and b = 1

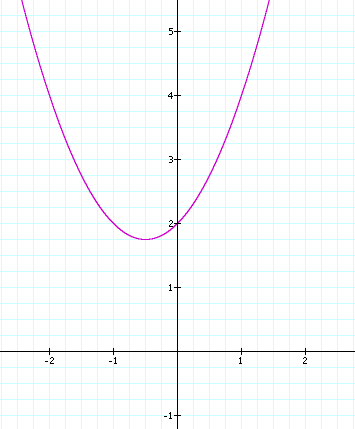
This is the same as the graph for the following equation:

where c=2.

What happens to this graph when the variable ‘a’ is varied?

Let’s set a equal to the following values:

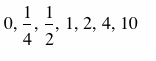
The following graphs result:

 

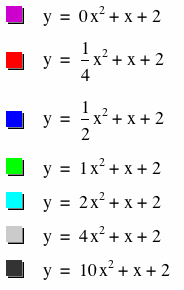
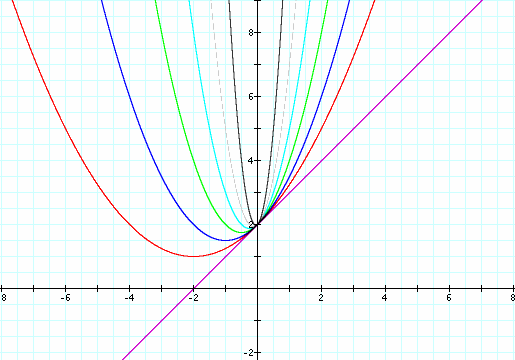
When a = 0, the graph is a line that intersects the y axis at 2 and has a slope of 1.

This is consistent with plugging 0 in for a. The above equation becomes

Which equals

And since b=1 and c=2, the equation of the line becomes

As a increases in value, the line above changes into a parabola with the axis of symmetry as a negative x-value.

Further increases in the value of a result in the vertical stretching of the parabola and the vertex approaching the intersection with the y-axis

 

Let’s also look at what happens when a < 0. We will set a equal to the following values:

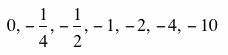
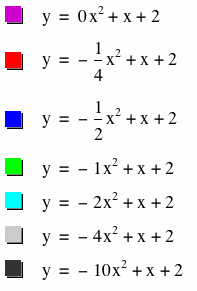
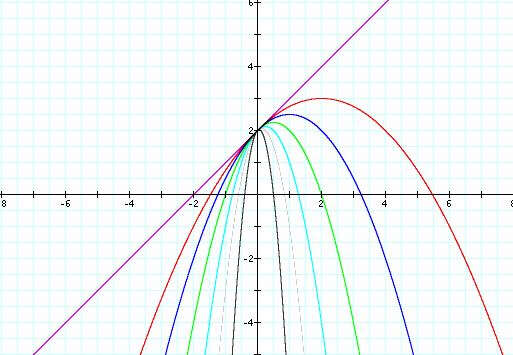
As a decreases in value from 0, the line changes into a parabola that opens down with the axis of symmetry as a positive x-value.

Further decreases in the value of a result in the vertical stretching of the parabola and the vertex approaching the intersection with the y-axis.

 

How does the change in a affect the shape of other graphs? Here are animations of variations in a for various graphs.