William Plummer - Assignment 3

Examine the following equation:

This equation is the standard quadratic equation where a = 1, and c = 1 over various values for b

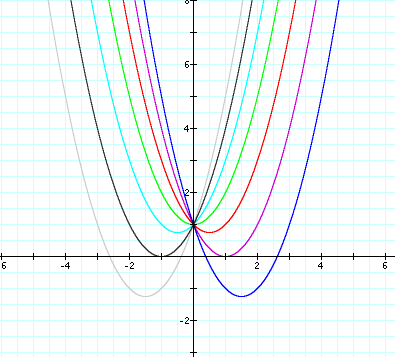
To graph this relation in the xb plane in Graphing Calculator we substitute a y for the b in the original equation.

So now we are graphing the following equation.

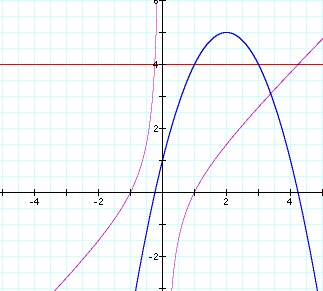
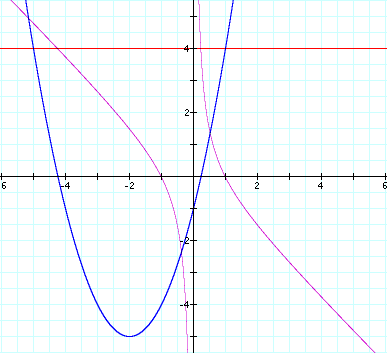
If we let b = 5 in the original equation and overlay that graph (y=5 for the graph in the xb plane), then we have a horizontal line that intersects the curve at two points.

These points correspond with the roots obtained when we set b equal to the same value on the xy plane

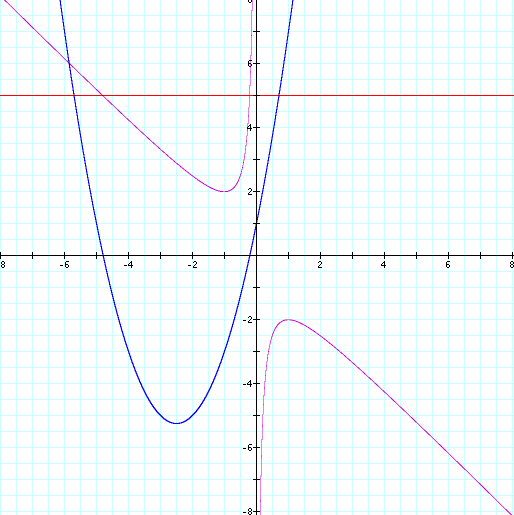
It is easy to see that the x values of the intersections for any value of b in the xb plane are the same as the x values where the parabola intersects the x-axis.

We can observe the following results for different values for b:

b > 2 results in 2 negative real roots

b = 2 results in one negative real root

-2 < b < 2 results in no real roots

b = -2 results in one positive real root

b < -2 results in two positive real roots .

What happens when take the original equation and change the value of c from +1 to -1?

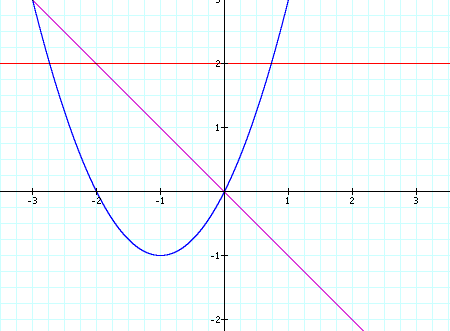
In the xy plane, the parabola shifts down and now intersects the y-axis at y = -1.

When we change the value of b in this new equation, the parabola always intersects the x-axis in two places, so there two real roots across all values of b.

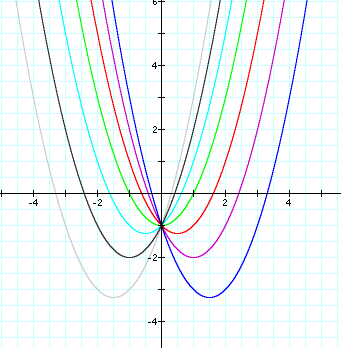
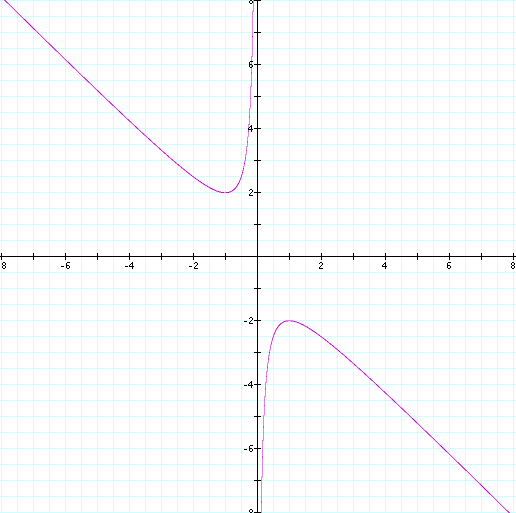
When we examine our new relation in the xb plane, we see that the shape of our curve has changed.

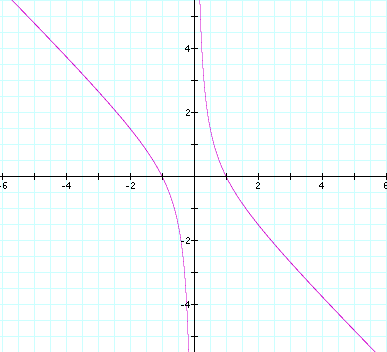
When we overlay the graph of b = k for any value of k, the graph intersects our curve in two places over all values of k, (and therefore, all values of b)

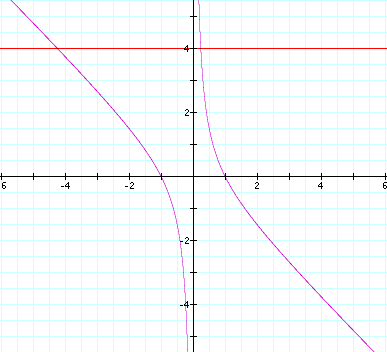
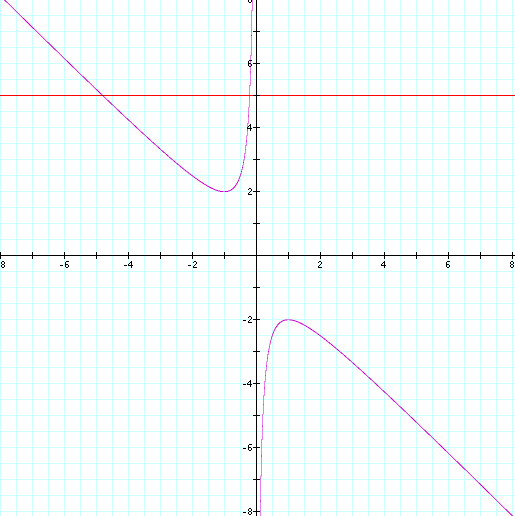
When we look at the graphs of both xy and xb, we see the corresponding roots of the parabola and the intersection of the curve with the graph of b = k for all values of k.

How about when c = 0?

When c = 0, the parabola intersects the y-axis at the origin where y = 0. This point serves as a constant root (x = 0) whenever c = 0. It is the only root when b = 0.

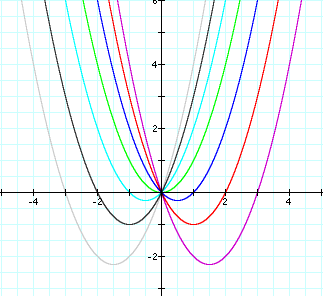
As the value of b changes, the equation has two roots, one at x = 0 and one at x = -b

Let’s see the xy plane overlayed by the xb plane

What happens when a a negative value?

Our original equation changes to the following:

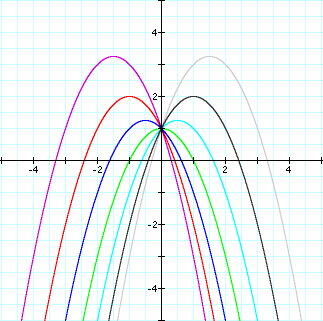
When the value of a is negative, our parabola still intersects the y axis where y = c, but now it opens down. Since the parabola intersects the y-axis at a positive value and opens down, it always results in two real roots.

Let’s see the parabola overlayed with the xb plane