Assignment #4

Let’s look at a triangle and construct the altitude for each vertex.

The altitude is the segment that goes through the vertex and is perpendicular to the side opposite that vertex. It is used to find the area of a triangle, for the area of a triangle is equal to the product of half the length of the base and the altitude.

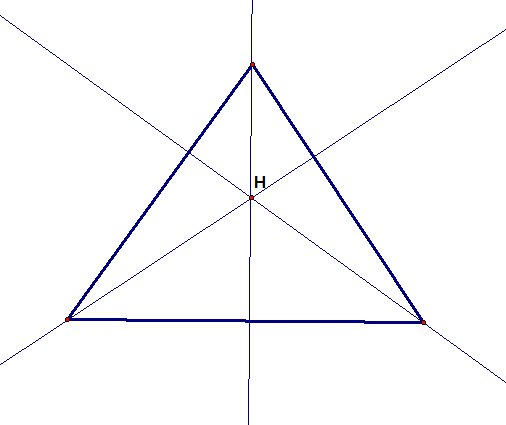
Now let ‘s construct the altitudes for the other two vertices of the triangle.

Notice that all three altitudes intersect at the same point. This point is called the Orthocenter.

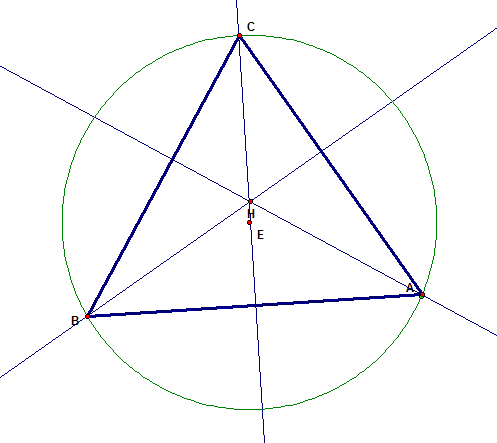
As in the diagram above, the Orthocenter is located inside the triangle only when the triangle is acute, when all of the angles are less than 90 degrees.

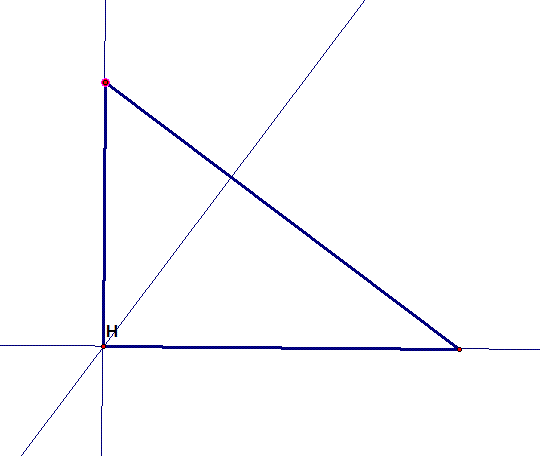
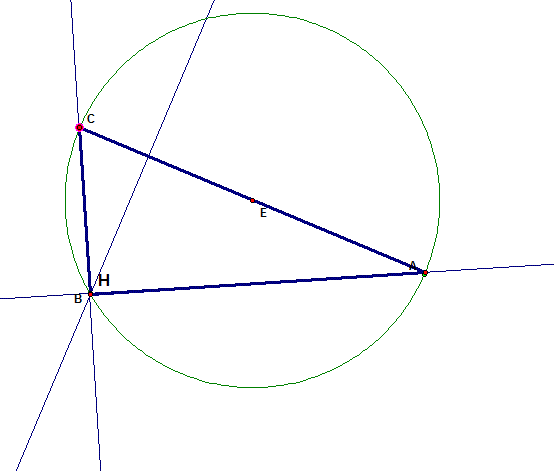
When the triangle is a right triangle, the orthocenter lies directly on the vertex of the right angle.

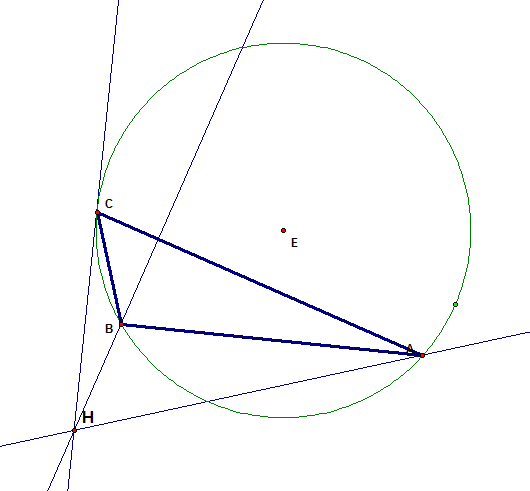
When the triangle has an obtuse angle, the orthocenter lies outside the triangle.

Let’s look at the behavior of the orthocenter as a triangle changes shape.

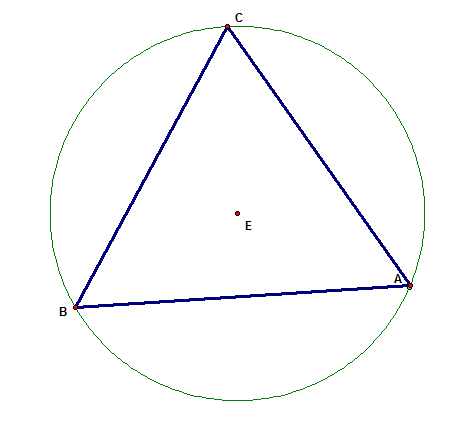
First let’s inscribe a triangle inside a circle.

Now let’s construct the orthocenter as we did earlier

As we move one of the vertices, the position of the altitudes change, and therefore, the position of the orthocenter is also changed. As long as all three angles in the triangle are acute, the orthocenter lies inside the triangle.

We can confirm that the orthocenter does approach the right angle in a right triangle by observing the orthocenter as one of the vertices is moved about the circle. We know that a right triangle inscribed in a circle has its hypotenuse crossing the center of the circle, so when we have a side that does intersect the center of the circle, the orthocenter is located at the vertex opposite the hypotenuse.

As the right angle increases in measure, the orthocenter crosses the vertex of that right triangle and lies outside the triangle.

Click here for a GSP sketch of the inscribed triangle and its orthocenter. Drag the vertices to change the shape of the triangle, and therefore, the location of the orthocenter.