Assignment 6

Given three points A, B, and C, we will draw a line that intersects segment AC at point X and also intersects segment BC at point Y such that

AX = XY = YB

Let’s create an angle ABC as follows

For now we’ve left off point B and have a dashed line that intersects point C. Point B will be on that line, but we do not know exactly where yet. We will find it as our last step.

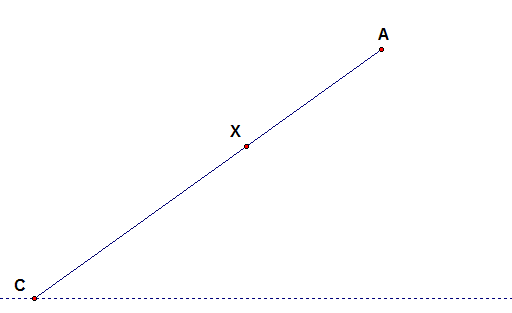
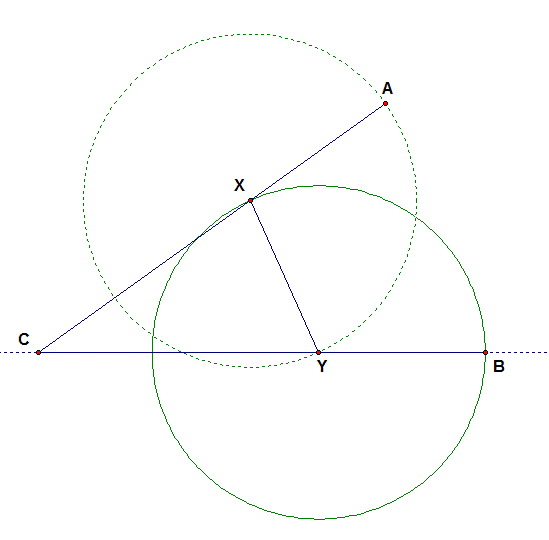
To start off, we can place an arbitrary point on segment AC and call that point X.

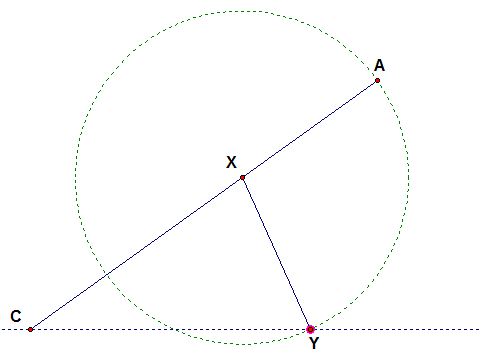
Next we need to take the distance from X to A and translate that distance from X to an intersection with BC. We can do that by creating a circle with its center at point X and point A on its circumference.

The distance from X to A is the radius of the circle and is the same as the distance from X to any point on that circle. To translate the length of AX to BC we look at the intersection point between the circle and segment BC and call that point Y. We now construct the segment XY. Since point Y is on the circle, and all radii of a circle are congruent, we can conclude that AX = XY.

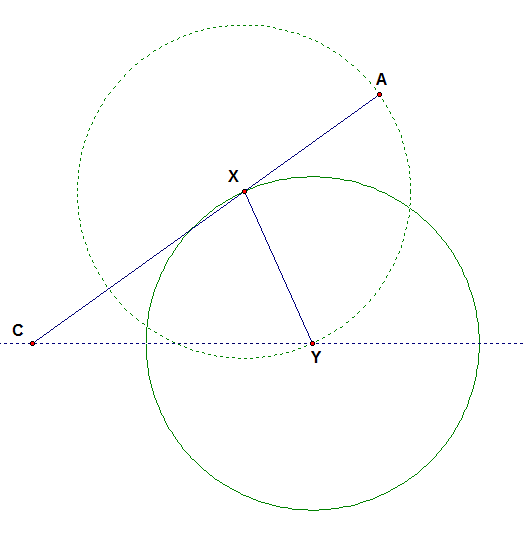
The final step is to translate the length of XY (which is the same length of AX) along the line from point C so that we can locate our point B. We do this by creating another circle with Y as its center and point X on its circumference.

Since XY is the radius of our first circle and also a radius of our second circle, we can conclude that both circles are congruent. We can also conclude that any radius from our first circle will be congruent with any radius from our second circle. To locate our point B, we look at the intersection point between our second circle and the dashed line from point C. We can call this intersection point B.

So now we have a line that intersects segment AC at point X and also intersects segment BC at point Y such that

AX = XY = YB