Sectors of Circles
According to Webster-Merriam’s Dictionary, we can define a sector of a circle to be defined as, “a geometric figure bounded by two radii and the included arc of a circle.” The diagram below provides a visual representation of a sector of a circle.
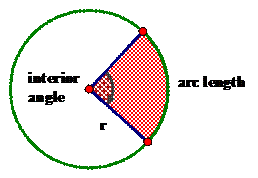
Since we know the area of a circle, and the circumference of a circle, we can find out some way to relate the area of a sector, as well as the arc length of a sector, in terms of the radius length and the central angle the sector has created.
When looking at the area of the sector, we know that the
area of a circle is ![]() .
But, we are trying to find the area of some portion of the circle. Given any
sector, there will always be some proportion that represents the proportion of
the sector to the whole circle. When
looking at angle measure, it is safe to say that the angle measure of the
central angle created by some sector is also some proportion of the angle
measure of the whole entire circle. So knowing this, we can manipulate the
formula for a circle to find the area of a sector. Given the angle measure of
the central angle in degrees, we can determine the proportion of the circle
that has been cut out by the sector.
.
But, we are trying to find the area of some portion of the circle. Given any
sector, there will always be some proportion that represents the proportion of
the sector to the whole circle. When
looking at angle measure, it is safe to say that the angle measure of the
central angle created by some sector is also some proportion of the angle
measure of the whole entire circle. So knowing this, we can manipulate the
formula for a circle to find the area of a sector. Given the angle measure of
the central angle in degrees, we can determine the proportion of the circle
that has been cut out by the sector.
So, say the interior angle measure (in
degrees) is 125°. Then we know that 125°/360° is the proportion of the circle
cut out by the sector. To find the area of this sector, we can take the area of
the whole circle, and multiply it by the proportion of the circle the sector
cuts out. In this case, the area of the sector with a central angle measure of
125° is (125°/365°)![]() .
.

In general, the area of a sector of a
circle in terms of the measure of the central angle of the sector is (x/360°)![]() .
.
With a similar thought process, we can
determine the arc length of a sector of a circle by manipulating the formula
for the circumference of a circle, which is C=2![]() .
When looking at this formula, we see
that essentially, the circumference is the radius length, multiplied by the angle
measure of the circle in radians, which is 2
.
When looking at this formula, we see
that essentially, the circumference is the radius length, multiplied by the angle
measure of the circle in radians, which is 2![]() So,
if we want to find the arc length of a sector, we can take the proportion of
the angle measure of the sector in relation to the angle measure of the circle,
and multiply it by the radius length. Using
the previous example, let the sector of a circle be 125°, or (25/36)π. Then, we can multiply this fraction by the radius
length to obtain the arc length of the sector.
So,
if we want to find the arc length of a sector, we can take the proportion of
the angle measure of the sector in relation to the angle measure of the circle,
and multiply it by the radius length. Using
the previous example, let the sector of a circle be 125°, or (25/36)π. Then, we can multiply this fraction by the radius
length to obtain the arc length of the sector.

In general, the arc length for a sector
of a circle in terms of the central angle of the sector is (x/360°)r (x in degrees) or (x/2π)r (x in radians).
Return to EMAT 4690/6690 Home page