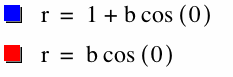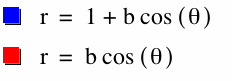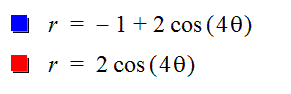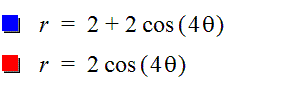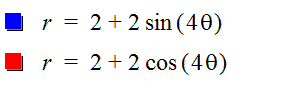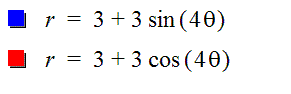Rayen Antillanca.
Assignment 11
The
polar coordinate system is a two dimensional coordinate system in which
each point on a plane is determined by a distance from a fixed point and an
angle from a fixed direction.
The
fixed point (analogous to the origin of a Cartesian system) is called the pole,
and the ray from the pole in the fixed direction is the polar axis. The
distance from the pole is called the radial coordinate or radius,
and the angle is the angular coordinate, polar angle.
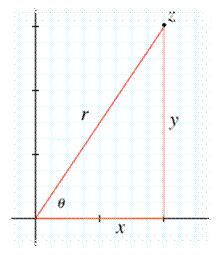
The equations which connect
the Cartesian coordinates with the polar coordinates are the next:
![]()
![]()
Now,
I am going to investigate the next equation
![]()
First
Investigation
|
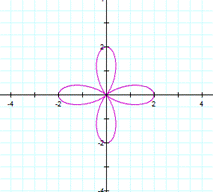
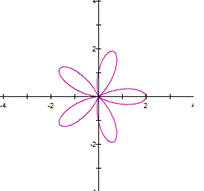
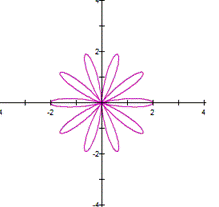
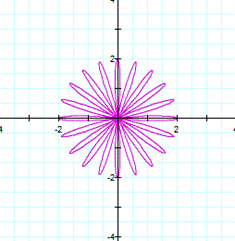
Let a=1, b=1 and
diferente values of k. Then |
|
|
When k varies from
negative integer values to positives integer values this happens |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
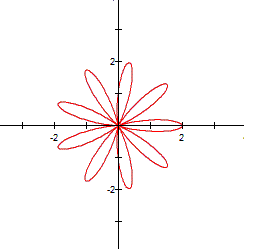
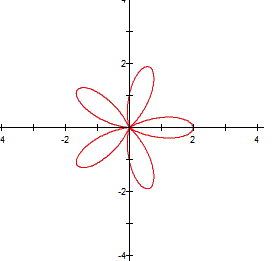
When
k varies, the equation takes the form of a flower which has k leaves. If
k>0 or k<0, it does not matter, the flower has the same number of leaf.
This occurs when a=b and k is an integer number. Some textbooks called this
n-leaf rose, where n=k. Actually the name is obvius, the form of the graph is
like a rose where k is the number of leaf. |
|
|
This rose curve
describe a family of curves where the length of the patals are the sum of a+b
when a=b For example you can
see the next image |
|
|
|
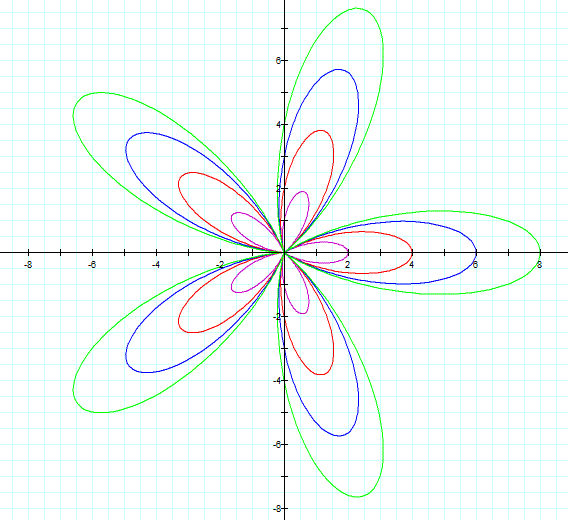
Where
the purple rose has 5 petals and the length of its leaf is 2, because a=1 The
length of the leaf of red one is 4, because a=2 The
length of the leaf of blue one is 6, because a=6 The
length of the leaf of green one is 8, because a=4 |
Second
Investigation
|
When a varies
and b=1 and k=1. Then
I am going to take small values for a |
|
|
|
|
|
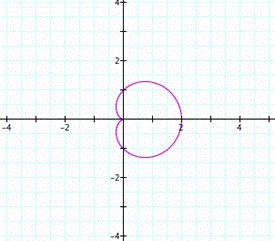
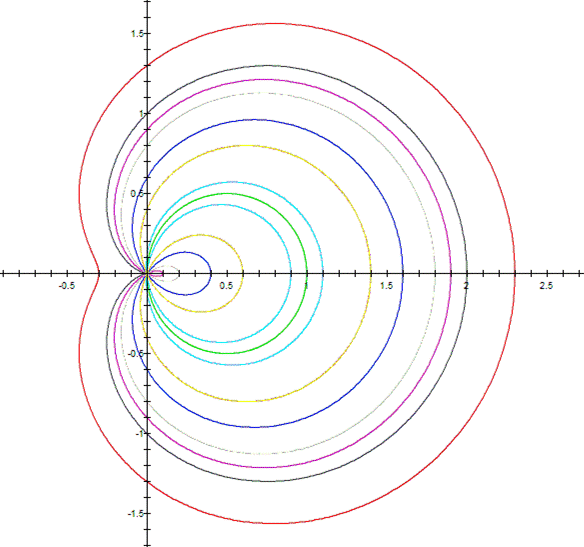
When a takes values
close to zero, the shape of the curve trends to a “smooth heart”. When the values
begin to move away from zero, this curve trends to a take circular shape. When b=1 and k=1, these curves as
known as limacon, which is defined as a roulette
formed when a circle rolls around the outside of a circle of equal radius. It
can also be defined as the roulette formed when a circle rolls around a
circle with half its radius so that the smaller circle is inside the larger
circle. Thus, they belong to the family of curves called centered trochoids. |
|
Third
Investigation
|
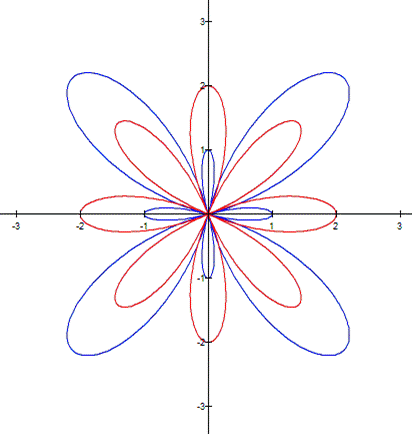
Now, I am going to compare two
different equations
|
|
|
|
|
|
|
|
|
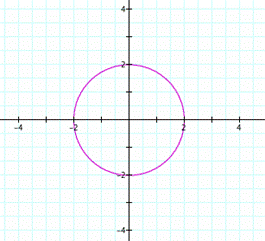
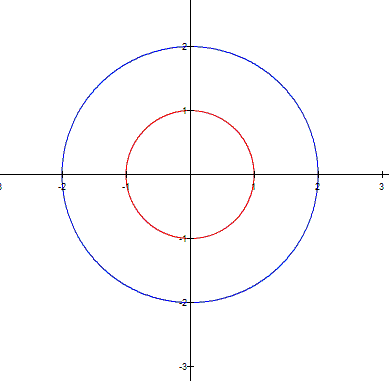
The blue curve has
the form of circle, the red one also. Why? As b=1, and cos(0)=1
in the red circle the radius is 1, and in the red circle the radious is 2. |
The red curve is
still a circle but the blue curve is a limacon. |
|
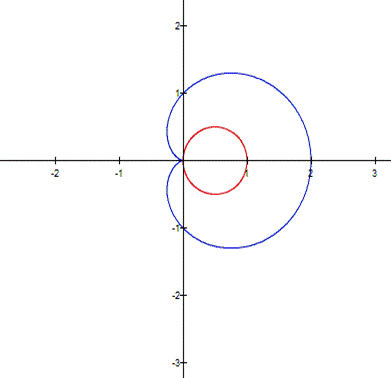
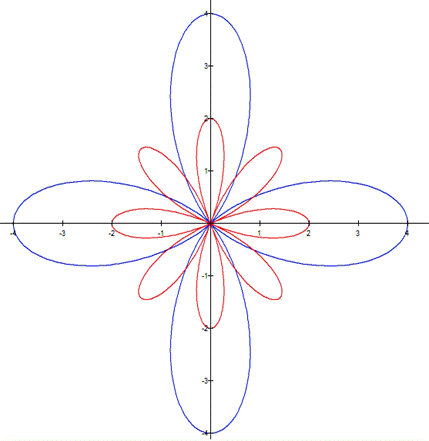
Another comparison |
|
|
|
|
|
|
|
|
As you can see, the
both curves have a flower-like shape |
|
Fourth
Investigation
|
If cos() is
replaced by sin() |
|
|
|
|
|
|
|
|
|
|
|
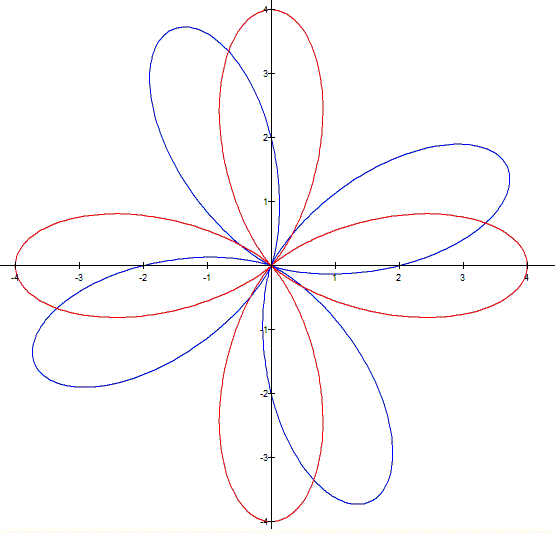
If I replace cos()
by sin() this two functions have the same flower-like shape. But, the blue
flower is rotated around the origin with respect to the red flower. |
|
|
Note: All graphs of this webpage were made with
Graphing Calculator 4.0 |