http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/EMAT6680.gif

Rayen Antillanca. Assignment 12

Generate a Fibonnaci sequence in the first column using f(0) = 1, f(1) = 1,f(n) = f(n-1) + f(n-2)

 

 

Fibonnaci Sequence

n

Fibonnaci Sequence

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image011.gif

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image015.gif

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image018.gif

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image020.gif

1

1

2

1

1

3

2

2

2

4

3

1.5

3

3

5

5

1.666667

2.5

5

5

6

8

1.6

2.666667

4

8

7

13

1.625

2.6

4.333333

6.5

8

21

1.615385

2.625

4.2

7

9

34

1.619048

2.615385

4.25

6.8

10

55

1.617647

2.619048

4.230769

6.875

11

89

1.618182

2.617647

4.238095

6.846154

12

144

1.617978

2.618182

4.235294

6.857143

13

233

1.618056

2.617978

4.236364

6.852941

14

377

1.618026

2.618056

4.235955

6.854545

15

610

1.618037

2.618026

4.236111

6.853933

16

987

1.618033

2.618037

4.236052

6.854167

17

1597

1.618034

2.618033

4.236074

6.854077

18

2584

1.618034

2.618034

4.236066

6.854111

19

4181

1.618034

2.618034

4.236069

6.854098

20

6765

1.618034

2.618034

4.236068

6.854103

21

10946

1.618034

2.618034

4.236068

6.854101

22

17711

1.618034

2.618034

4.236068

6.854102

23

28657

1.618034

2.618034

4.236068

6.854102

24

46368

1.618034

2.618034

4.236068

6.854102

25

75025

1.618034

2.618034

4.236068

6.854102

26

121393

1.618034

2.618034

4.236068

6.854102

27

196418

1.618034

2.618034

4.236068

6.854102

28

317811

1.618034

2.618034

4.236068

6.854102

29

514229

1.618034

2.618034

4.236068

6.854102

30

832040

1.618034

2.618034

4.236068

6.854102

31

1346269

1.618034

2.618034

4.236068

6.854102

32

2178309

1.618034

2.618034

4.236068

6.854102

33

3524578

1.618034

2.618034

4.236068

6.854102

34

5702887

1.618034

2.618034

4.236068

6.854102

35

9227465

1.618034

2.618034

4.236068

6.854102

 

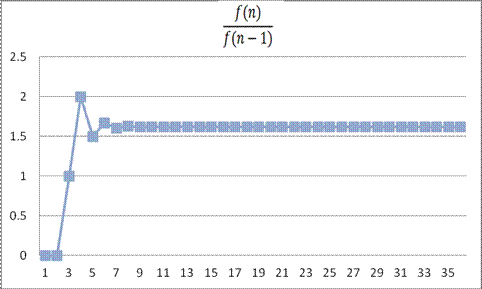
The next graphs show what happens when n increases.

When n increases, the first ratio, the ratio between each adjacent pair of numbers in the Fibonnaci Sequence, is approaching to 1.618033089 which is the Golden Ratio

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image022.gif

 

 

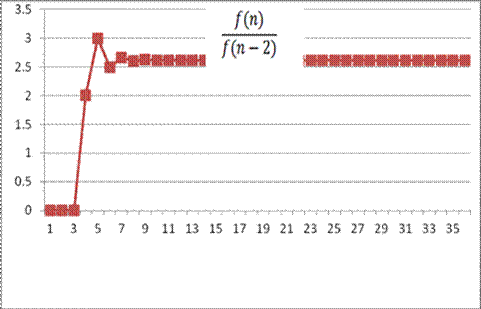
When n increases, the first ratio, the ratio between the n-th and the

 (n-2)-th terms of the Fibonnaci Sequence, is approaching to 2.618033989 which is the square of Golden Ratio

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image024.gif

 

 

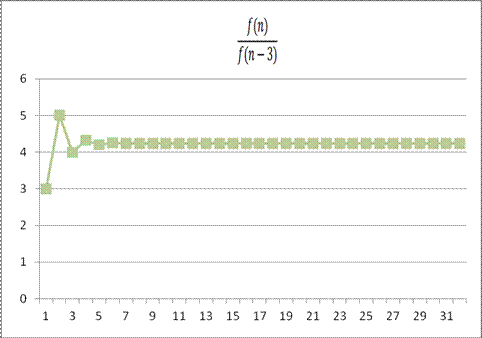
When n increases, the first ratio, the ratio between the n-th and the

 (n-3)-th terms of the Fibonnaci Sequence, is approaching 4.236067977 which is the cubic of Golden Ratio.

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image025.gif

 

 

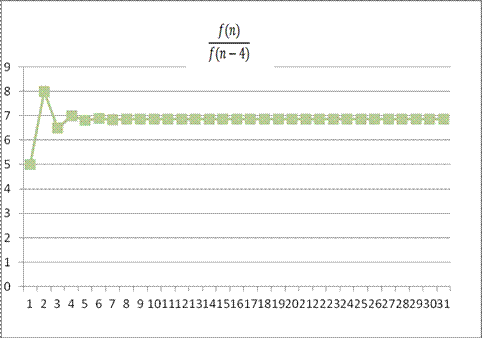
When n increases, the first ratio, the ratio between the n-th and the

 (n-4)-th terms of the Fibonnaci Sequence, is approaching 6.854101966

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image026.gif

 

Therefore, as n increases, we observe that the limits of the ratios above explored correspond to the Golden Ratio, Square of Golden Ratio, Cubic Golden Ratio, 4th power of Golden Ratio, etc. respectively.

 

 

 

Lucas Sequence

n

Lucas Sequence

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image011.gif

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image015.gif

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image018.gif

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image020.gif

1

3

3

2

4

1.333333

4

3

7

1.75

2.333333

7

4

11

1.571429

2.75

3.666667

11

5

18

1.636364

2.571429

4.5

6

6

29

1.611111

2.636364

4.142857

7.25

7

47

1.62069

2.611111

4.272727

6.714286

8

76

1.617021

2.62069

4.222222

6.909091

9

123

1.618421

2.617021

4.241379

6.833333

10

199

1.617886

2.618421

4.234043

6.862069

11

322

1.61809

2.617886

4.236842

6.851064

12

521

1.618012

2.61809

4.235772

6.855263

13

843

1.618042

2.618012

4.236181

6.853659

14

1364

1.618031

2.618042

4.236025

6.854271

15

2207

1.618035

2.618031

4.236084

6.854037

16

3571

1.618034

2.618035

4.236062

6.854127

17

5778

1.618034

2.618034

4.23607

6.854093

18

9349

1.618034

2.618034

4.236067

6.854106

19

15127

1.618034

2.618034

4.236068

6.854101

20

24476

1.618034

2.618034

4.236068

6.854102

21

39603

1.618034

2.618034

4.236068

6.854102

22

64079

1.618034

2.618034

4.236068

6.854102

23

103682

1.618034

2.618034

4.236068

6.854102

24

167761

1.618034

2.618034

4.236068

6.854102

25

271443

1.618034

2.618034

4.236068

6.854102

26

439204

1.618034

2.618034

4.236068

6.854102

27

710647

1.618034

2.618034

4.236068

6.854102

28

1149851

1.618034

2.618034

4.236068

6.854102

29

1860498

1.618034

2.618034

4.236068

6.854102

30

3010349

1.618034

2.618034

4.236068

6.854102

31

4870847

1.618034

2.618034

4.236068

6.854102

32

7881196

1.618034

2.618034

4.236068

6.854102

33

12752043

1.618034

2.618034

4.236068

6.854102

34

20633239

1.618034

2.618034

4.236068

6.854102

35

33385282

1.618034

2.618034

4.236068

6.854102

Even though in the Lucas Sequence the ratios start at different numbers, as n increase the ratios approach to the same numbers of Fibonnaci Sequence: Golden Ratio, square of Golden Ratio, Cubic of Golden Ratio, 4th power of golden Ratio respectively.

Others sequences:

Sequence with http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image027.gif and http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image028.gif

n

Sequence

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image011.gif

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image015.gif

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image018.gif

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image020.gif

1

5

1.25

2

9

1.8

2.25

3

14

1.555556

2.8

3.5

4

23

1.642857

2.555556

4.6

5.75

5

37

1.608696

2.642857

4.111111

7.4

6

60

1.621622

2.608696

4.285714

6.666667

7

97

1.616667

2.621622

4.217391

6.928571

8

157

1.618557

2.616667

4.243243

6.826087

9

254

1.617834

2.618557

4.233333

6.864865

10

411

1.61811

2.617834

4.237113

6.85

11

665

1.618005

2.61811

4.235669

6.85567

12

1076

1.618045

2.618005

4.23622

6.853503

13

1741

1.61803

2.618045

4.23601

6.854331

14

2817

1.618036

2.61803

4.23609

6.854015

15

4558

1.618033

2.618036

4.236059

6.854135

16

7375

1.618034

2.618033

4.236071

6.854089

17

11933

1.618034

2.618034

4.236067

6.854107

18

19308

1.618034

2.618034

4.236068

6.8541

19

31241

1.618034

2.618034

4.236068

6.854103

20

50549

1.618034

2.618034

4.236068

6.854102

21

81790

1.618034

2.618034

4.236068

6.854102

22

132339

1.618034

2.618034

4.236068

6.854102

23

214129

1.618034

2.618034

4.236068

6.854102

24

346468

1.618034

2.618034

4.236068

6.854102

25

560597

1.618034

2.618034

4.236068

6.854102

26

907065

1.618034

2.618034

4.236068

6.854102

27

1467662

1.618034

2.618034

4.236068

6.854102

28

2374727

1.618034

2.618034

4.236068

6.854102

29

3842389

1.618034

2.618034

4.236068

6.854102

30

6217116

1.618034

2.618034

4.236068

6.854102

31

10059505

1.618034

2.618034

4.236068

6.854102

32

16276621

1.618034

2.618034

4.236068

6.854102

33

26336126

1.618034

2.618034

4.236068

6.854102

34

42612747

1.618034

2.618034

4.236068

6.854102

35

68948873

1.618034

2.618034

4.236068

6.854102

 

 

Sequence with http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image043.gifand http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image044.gif

n

1

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image011.gif

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image015.gif

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image018.gif

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image020.gif

1

7

7

2

8

1.142857

8

3

15

1.875

2.142857

15

4

23

1.533333

2.875

3.285714

23

5

38

1.652174

2.533333

4.75

5.428571

6

61

1.605263

2.652174

4.066667

7.625

7

99

1.622951

2.605263

4.304348

6.6

8

160

1.616162

2.622951

4.210526

6.956522

9

259

1.61875

2.616162

4.245902

6.815789

10

419

1.617761

2.61875

4.232323

6.868852

11

678

1.618138

2.617761

4.2375

6.848485

12

1097

1.617994

2.618138

4.235521

6.85625

13

1775

1.618049

2.617994

4.236277

6.853282

14

2872

1.618028

2.618049

4.235988

6.854415

15

4647

1.618036

2.618028

4.236098

6.853982

16

7519

1.618033

2.618036

4.236056

6.854148

17

12166

1.618034

2.618033

4.236072

6.854085

18

19685

1.618034

2.618034

4.236066

6.854109

19

31851

1.618034

2.618034

4.236069

6.854099

20

51536

1.618034

2.618034

4.236068

6.854103

21

83387

1.618034

2.618034

4.236068

6.854102

22

134923

1.618034

2.618034

4.236068

6.854102

23

218310

1.618034

2.618034

4.236068

6.854102

24

353233

1.618034

2.618034

4.236068

6.854102

25

571543

1.618034

2.618034

4.236068

6.854102

26

924776

1.618034

2.618034

4.236068

6.854102

27

1496319

1.618034

2.618034

4.236068

6.854102

28

2421095

1.618034

2.618034

4.236068

6.854102

29

3917414

1.618034

2.618034

4.236068

6.854102

30

6338509

1.618034

2.618034

4.236068

6.854102

31

10255923

1.618034

2.618034

4.236068

6.854102

32

16594432

1.618034

2.618034

4.236068

6.854102

33

26850355

1.618034

2.618034

4.236068

6.854102

34

43444787

1.618034

2.618034

4.236068

6.854102

35

70295142

1.618034

2.618034

4.236068

6.854102

 

Sequence with http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image045.gifand http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image046.gif

n

Sequence

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image011.gif

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image015.gif

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image018.gif

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image020.gif

1

3

-3

2

2

0.666667

-2

3

5

2.5

1.666667

-5

4

7

1.4

3.5

2.333333

-7

5

12

1.714286

2.4

6

4

6

19

1.583333

2.714286

3.8

9.5

7

31

1.631579

2.583333

4.428571

6.2

8

50

1.612903

2.631579

4.166667

7.142857

9

81

1.62

2.612903

4.263158

6.75

10

131

1.617284

2.62

4.225806

6.894737

11

212

1.618321

2.617284

4.24

6.83871

12

343

1.617925

2.618321

4.234568

6.86

13

555

1.618076

2.617925

4.236641

6.851852

14

898

1.618018

2.618076

4.235849

6.854962

15

1453

1.61804

2.618018

4.236152

6.853774

16

2351

1.618032

2.61804

4.236036

6.854227

17

3804

1.618035

2.618032

4.23608

6.854054

18

6155

1.618034

2.618035

4.236063

6.85412

19

9959

1.618034

2.618034

4.23607

6.854095

20

16114

1.618034

2.618034

4.236067

6.854105

21

26073

1.618034

2.618034

4.236068

6.854101

22

42187

1.618034

2.618034

4.236068

6.854102

23

68260

1.618034

2.618034

4.236068

6.854102

24

110447

1.618034

2.618034

4.236068

6.854102

25

178707

1.618034

2.618034

4.236068

6.854102

26

289154

1.618034

2.618034

4.236068

6.854102

27

467861

1.618034

2.618034

4.236068

6.854102

28

757015

1.618034

2.618034

4.236068

6.854102

29

1224876

1.618034

2.618034

4.236068

6.854102

30

1981891

1.618034

2.618034

4.236068

6.854102

31

3206767

1.618034

2.618034

4.236068

6.854102

32

5188658

1.618034

2.618034

4.236068

6.854102

33

8395425

1.618034

2.618034

4.236068

6.854102

34

13584083

1.618034

2.618034

4.236068

6.854102

35

21979508

1.618034

2.618034

4.236068

6.854102

 

Summary

As we can see, it does not matter which are the numbers  http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image047.gif  and http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment12/assignment12_files/image048.gif, the ratios are approaching to the same limits as those in the Fibonnaci Sequence, which are Golden Ratio, Square of Golden Ratio, Cubic Golden Ratio, 4th power of Golden Ratio respectively.

Why do the ratios in those sequences converge to the same limits as those of the Fibonnaci Sequence? It is because the Fibonnaci sequence is a recursive sequence, so it does not matter what the initial numbers are.

 

 

Note: All graphs on this webpage were made with Microsoft Office Excel

 

 

 

Rayen's Homepage