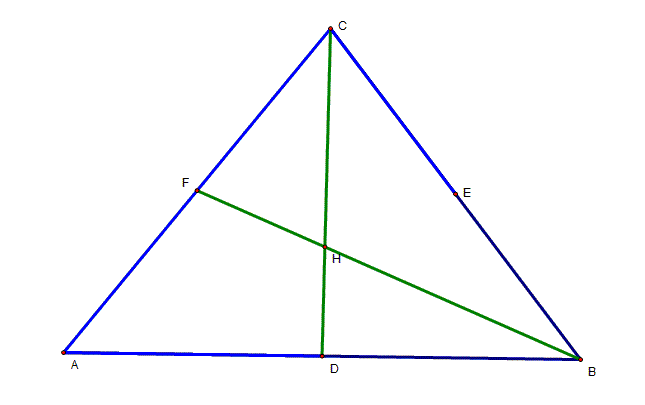Rayen Antillanca.
Assignment 4
|
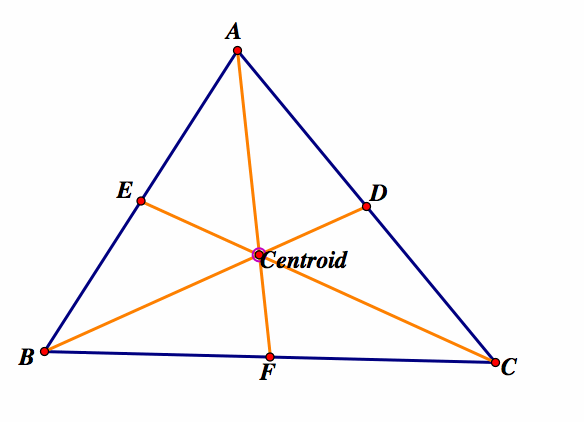
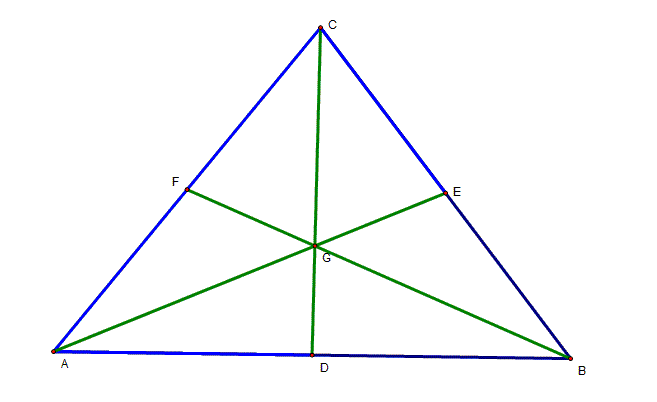
The centroid of the triangle is
the intersection of the three medians. Recall, a median of a triangle is a
line segment joining a vertex to the midpoint of the opposite side. Therefore
a triangle has three medians. |
|
|
The next explanation proves that these three medians are
concurrent.
|
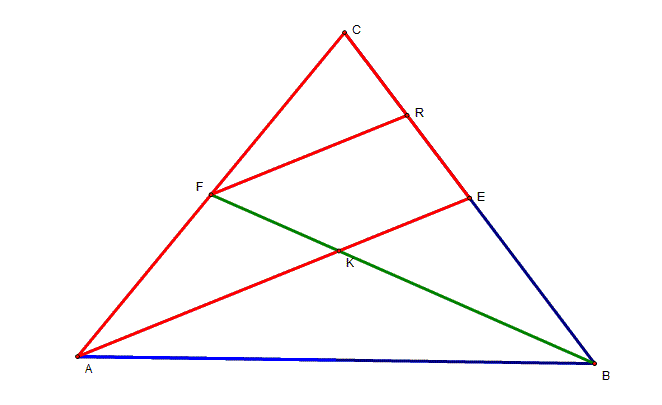
Step 1 Let ABC be any triangle, and let D,
E, and F be midpoints for the sides AC, AB and BC, respectively. The medians
from B and C meet at point G. |
|
|
|
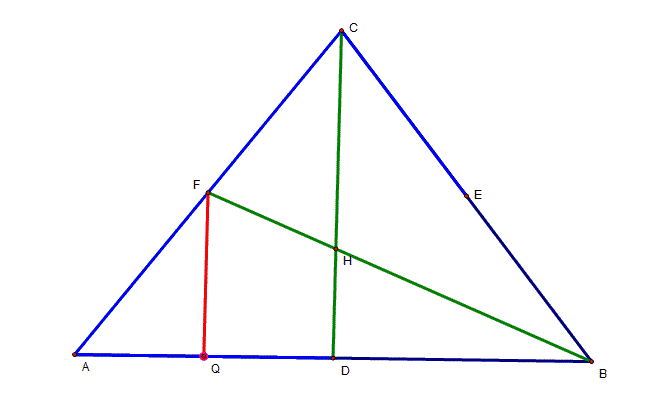
Step 2 Now, I draw a line parallel to DC
through F, and call Q its intersection with side AB |
|
|
|
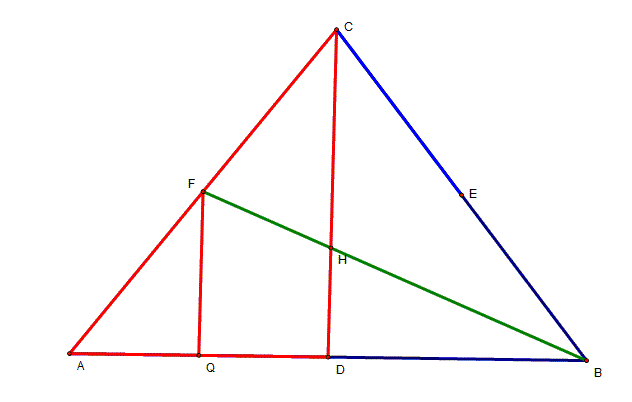
Step 3 The two triangles, ∆AQF and ∆ADC,
are similar, and so AF:AC:AQ:AD, which implies that
Q is the midpoint of AD. But AD=DB, so that QD:DB::1:2 and
since ∆QBF and ∆DBG are similar, the point G lies on median FB at
one-third its length from F. |
|
|
|
Step 4 Let K be the intersection of the two
medians AE and BF. I draw a line parallel to AE through F, and call R its
intersection with BC. The same argument in step 3 is used here to conclude
that the point K lies on median FB, at one-third its length from point F |
|
|
|
Step 5 This means that the two points, H and
K, are one and the same, so that the three medians are concurrent at a point,
say G. This completes the proof. G is the centroid. |
|
|
|
Summary |
|
The Centroid
(G) divides each median in the ratio 2:1, then the segment
from a vertex to the centroid is 2/3 of the median
from that vertex. To see an example in GSP of this fact
clic here |
|
Note: All figures on this web page were made with The Geometerís
Sketchpad |