Rayen Antillanca.
Assignment 7
Given two circles and a point on one of the circles. Construct a circle
tangent to the two circles with one point of tangency being the designated
point.
|
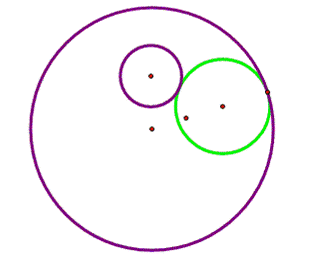
Figure 1 |
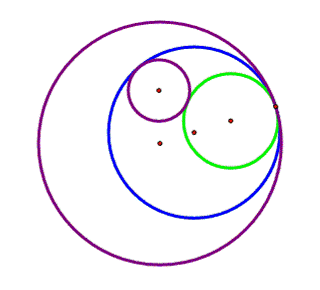
The green circle is
tangent to the two purple circles, and it does not surround the inside
circle. |
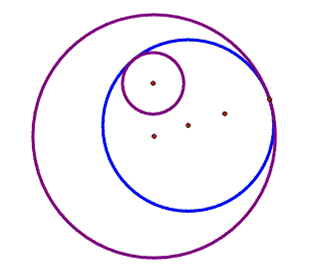
|
The blue circle is
also tangent to the two purple circles but it does surround the inside circle |
Figure 2 |
First
Investigation
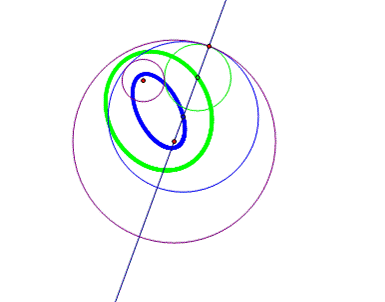
The locus of the tangent circle’s center is an ellipse, as it is shown
in red by figures 3 and 4.
|
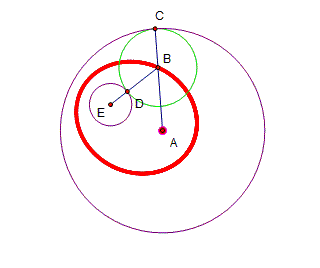
Figure 3 |
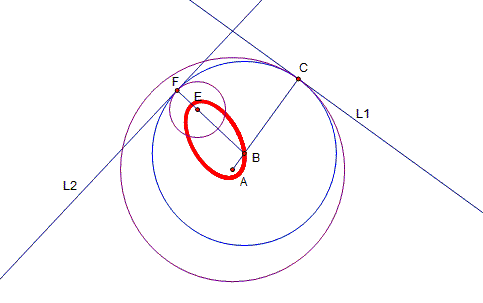
Figure 4 |
|
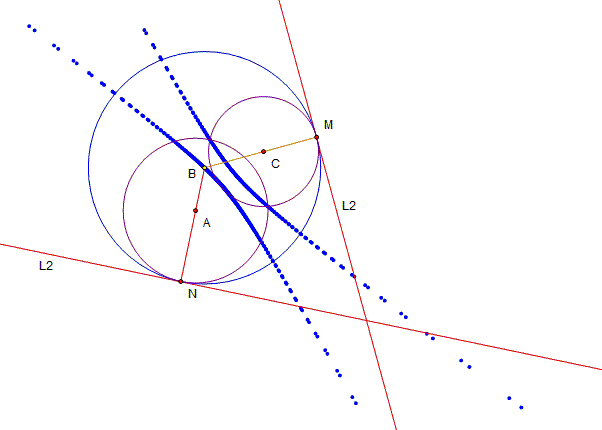
In
figure 3 we observe that BC = BD.
Then, we can see that AB + BE = constant since it is the sum of the
radii of the given circles. Thus, the
locus of B is in fact an ellipse by definition. In
figure 4, we may elaborate a similar argument to prove that the locus of B is
an ellipse. Let L1 be the tangent line through C, and let L2 be the tangent
line through F. L1 is perpendicular to the radius of the given circle with
center at A, and L2 is perpendicular to the radius of the given circle with
radius at E. Consequently, L1 and L2
are also perpendicular to the radii BC and BF, respectively, so that A, B,
and C and B, E, and F are collinear points, respectively. Finally, consider Since
BC and BF are radii, and consequently BC = BF, we obtain that The
relation (2) is constant because it is the subtraction between the radii of
the given circles. Consequently, the locus of B is an ellipse by definition. |
|
You
can explore the locus of figure 3 here
and the one in figure 4 here
|
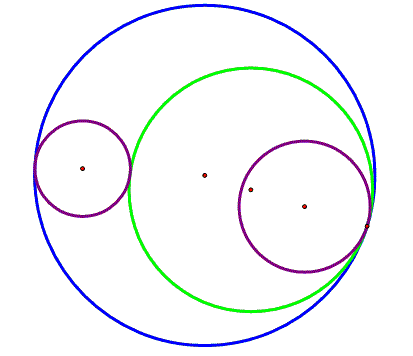
To complete the construction the next
picture shows the green and blue circles together. To draw this figure you can use this tool. |
Figure 5 |
|
The loci of the two tangent circles’ centers are two
ellipses, for the green circle is the green ellipse and for the blue circle
is the blue ellipse. |
|
Figure 6 |
|
With this animation, you could
explore the following situations: 1) What happens when the given
circles are tangent to each other, and the smallest one is inside of the
largest one? 2) What happens when the given
circles are tangent to each other, and the smallest one is outside of the
largest one? 3) What happens when the given
circles intersect to each other? 4) What happens when the given
circles do not intersect, and the smallest one is outside of the largest one? This animation
will permit you to explore this |
Second
Investigation
|
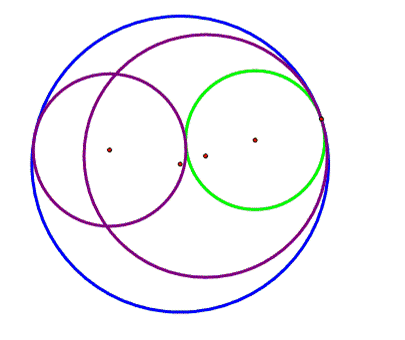
What happens with
these two tangent circles (green and blue) when the two given circles
(purple) intersect to each other? |
Figure 7 |
|
The loci the tangent circles’ centers
shown in figure 7 |
|
Figure 8 |
|
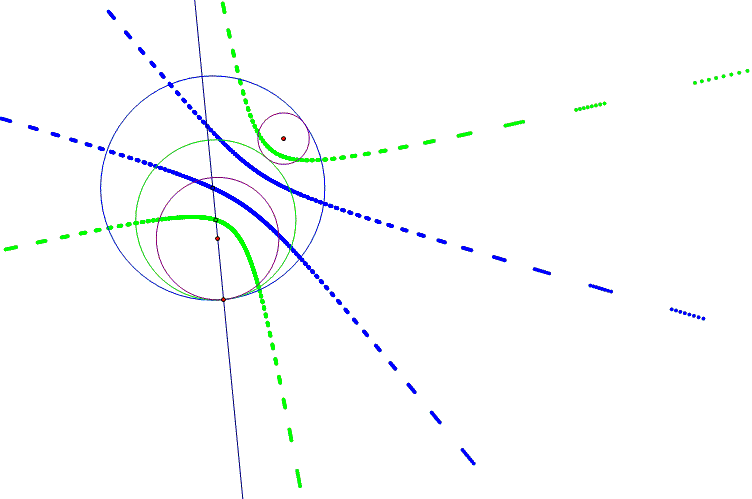
As
shown in the above figure, the locus of the green tangent circle’s center is
an ellipse, while the locus of the blue tangent circle’s center seems to be a
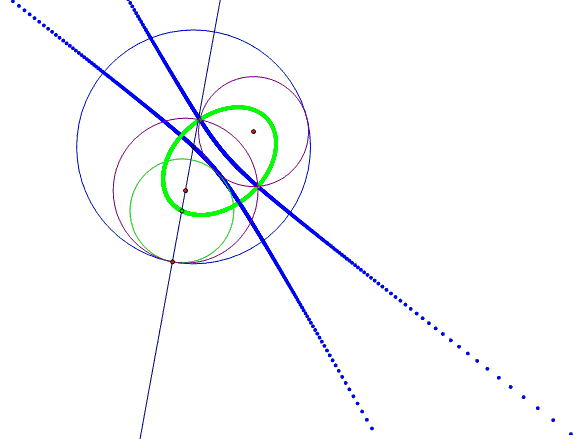
“know curve.” It is easy to show that the latter locus is a hyperbola. Consider the Figure 9 shown below: |
|
Figure 9 |
|
Let L1 be the tangent line through
M, and let L2 be the tangent line through N.
L1 is perpendicular to the radius of the given circle with center at
C, and L2 is perpendicular to the radius of the given circle with radius at
A. Consequently, L1 and L2 are also
perpendicular to the radii BM and BN, respectively, so that B, C, and M and
B, A, and N are collinear points, respectively. Finally, consider
Since BM and BN are radii, and
consequently BM = BN, we obtain that
The relationship (2) is constant
because it represents the subtraction between the radii of the given
circles. Therefore, the trace of the
blue tangent circle’s center is a hyperbola by definition. |
|
This
animation
will permit you to explore this. |
Third
Investigation
|
What happens when
the two given circles (purple) are completely separate from each other? Here
the green circle passes between the two given circles. The blue circle
encircles the both given circles. |
Figure 10 |
|
The loci the tangent circles’ centers
shown in figure 9 |
|
Figure 11 |
|
As the trace of the
centers of the green and the blue circles show, the loci of the green
circle’s center and the blue circle’s center are both hyperbolas. This animation
will permit you to explore this |
|
Note: All figures and tools on this web page were made with The
Geometer’s Sketchpad |