Rayen Antillanca.
Assignment 8
The
orthocenter
|
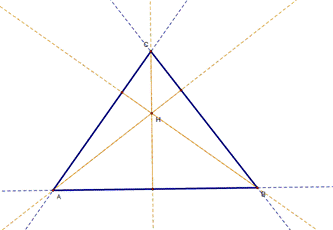
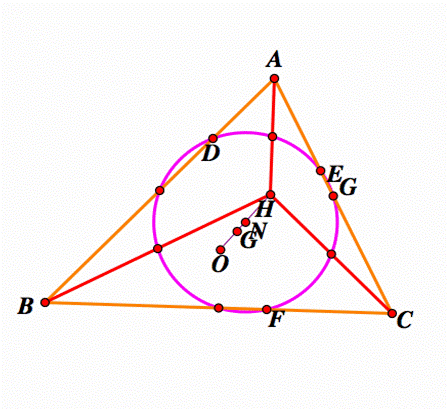
H is the orthocenter of ABC triangle.
The orthocenter of a triangle is the point of concurrency of the three lines
taken from a vertex of the triangle and perpendicular to the line of the
opposite side. The orthocenter is inside of the
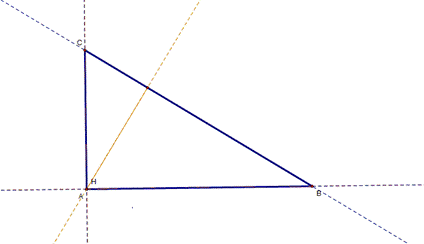
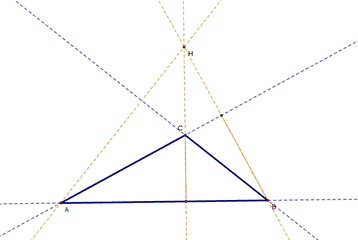
triangle if the triangle is acute; the orthocenter coincides with the vertex
of the angle if the triangle is right, and the othocenter
is outside of the triangle if the triangle is obtuse. |
||
|
Acute triangle |
Right triangle |
Obtuse triangle |
|
|
|
|
|
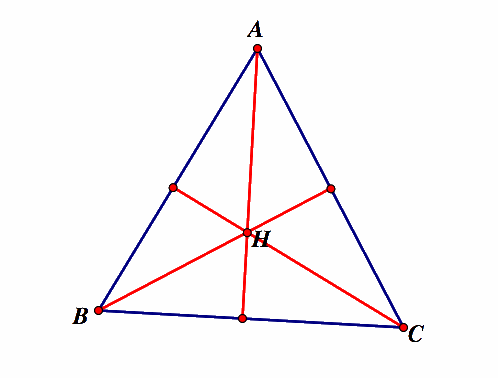
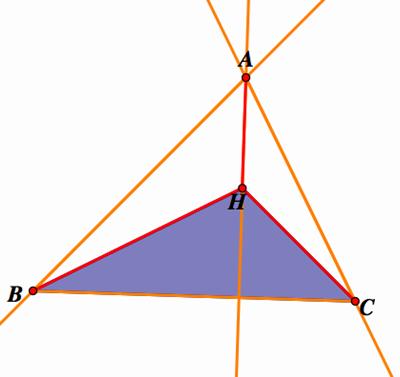
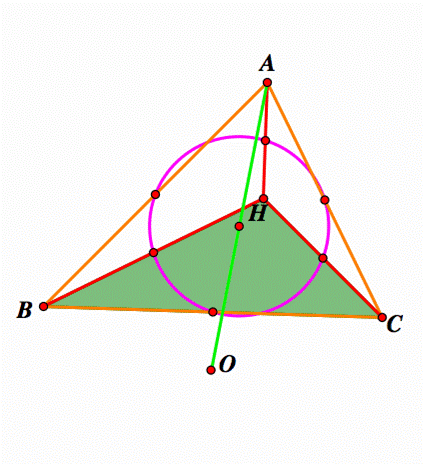
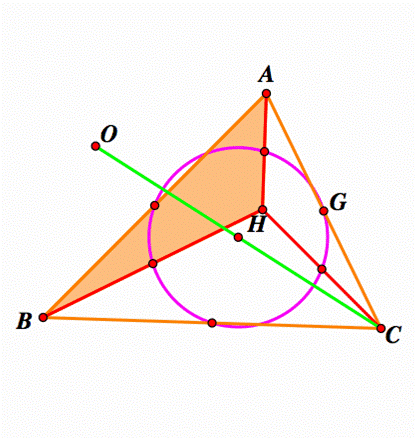
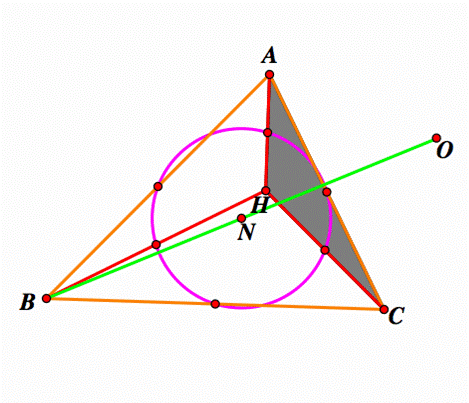
Given the ABC acute triangle
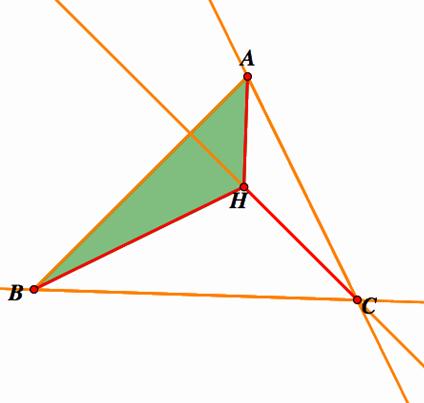
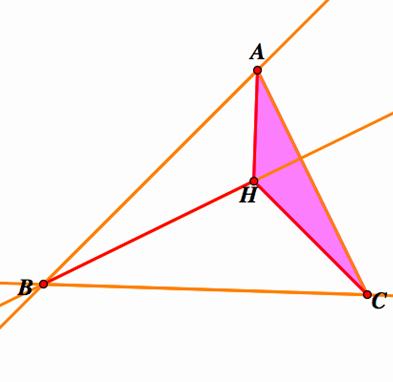
Where H is the orthocenter. The orthocenter of triangle HBC is
the vertex A, the Orthocenter of triangle HAB is the vertex C and the
Orthocenter of triangle HAC is the vertex B. Why? As of these triangle are
obtuse triangles, the orthocenter is outside of them and coincide with the
opposite vertex. I will show this fact in the figures
below |
||||
|
The
orthocenter of triangle HBC is vertex A |
The
orthocenter of triangle HAB is the vertex C |
The
orthocenter of triangle HAC is the vertex B |
||
|
|
|
|
|
|
|
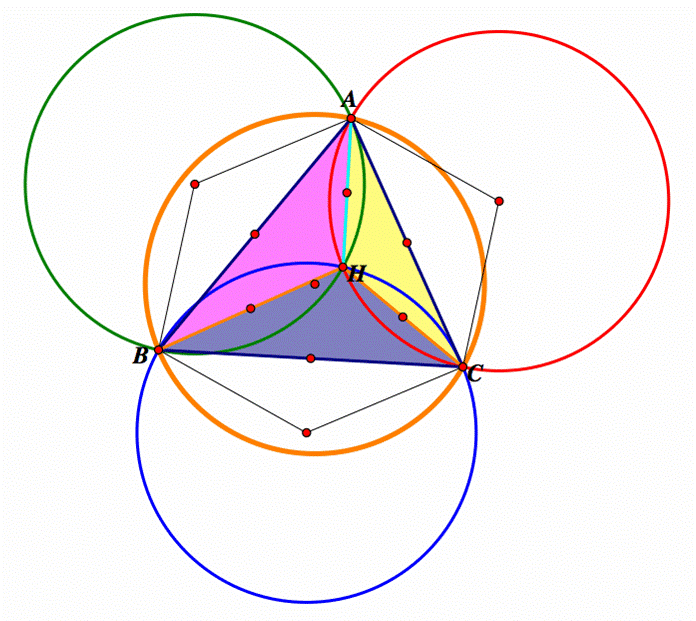
If I draw the circumcircle of triangles ABC, HBC, HAB, HAC, the result is
the next image. Recall, the circumcircle is the
circle which passes through all three vertices of a triangle |
|
|
When
the orthocenter coincides with a vertex of the triangle ABC, all the triangles
HBC, HAB, and HAC coincide with the triangle ABC. Similarly, all the circumcircles coincide with triangle ABCís circumcircles.
To
see this, you can explore here.
The
nine point circle
The
nine point circle gets its name because it passes through nine significant
points of a triangle. These points are:
∑
The midpoints of each side of the
triangle
∑
The foot of each altitude
∑
The midpoint of the line segment that
joints each vertex to the orthocenter.
|
The
nine point circle of the acute triangle ABC is: |
|
|
The next images show the nine circle
for triangle HBC, HAB, and HAC |
||||
|
Triangle
HBC |
Triangle HAB |
Triangle HAC |
||
|
|
|
|
|
|
As
you can see, these triangles have the same nine point circle. With the next
tool, you can draw the nine point
circle.
|
Note: All figures and tools on this web page were made with The
Geometerís Sketchpad |