Rayen Antillanca.
Assignment 9
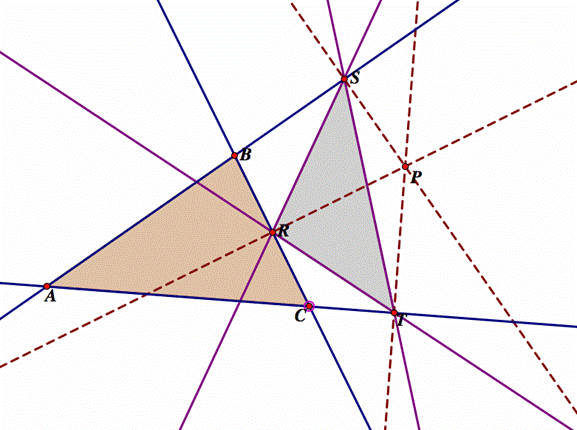
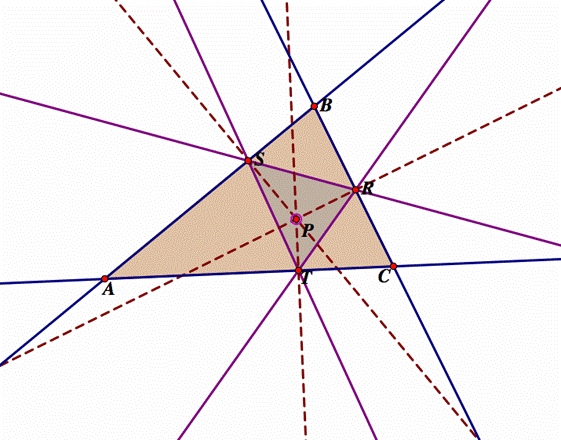
Let ABC be any triangle, and let P be any point on the
plane. From P construct perpendiculars lines to the sides of triangle ABC. Let
R, S, and T be the intersection points between the sides of the triangle ABC
and the perpendicular lines from P, as shown in figure below. Triangle RST is
the Pedal Triangle for Pedal Point P.
|
The triangle RST is the pedal triangle. Point P is outside
of triangle ABC |
|
|
The triangle RST is the pedal triangle. Point P is inside
of the triangle ABC |
|
If
you want to draw a pedal triangle, you can use this GSP tool.
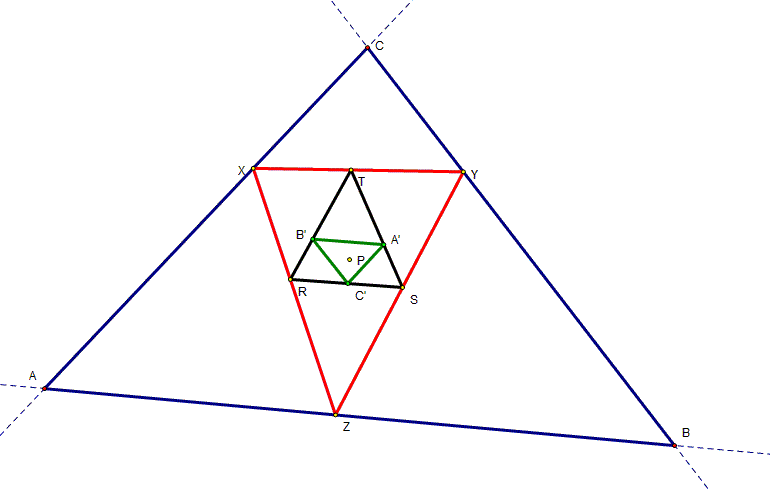
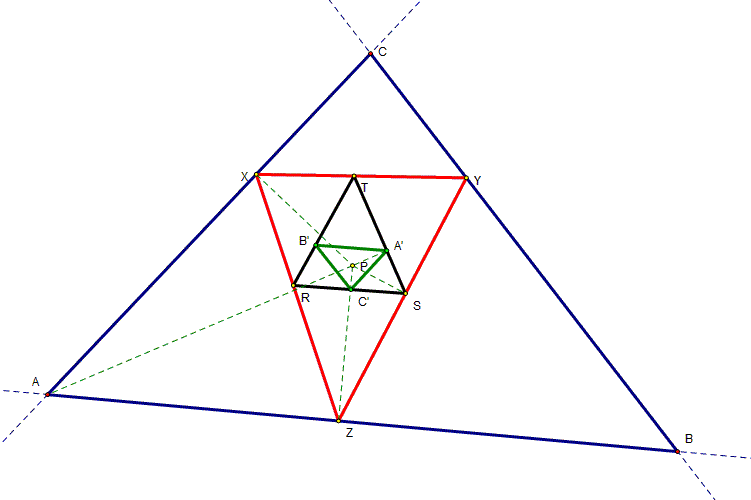
Prove the pedal
triangle of a pedal triangle of a pedal triangle of a point is similar to the
original triangle.
|
That is, show that
the pedal triangle A'B'C' of pedal triangle RST of the pedal triangle XYZ of
pedal point P is similar to the triangle ABC. |
|
|
|
Step 1 |
|
|
|
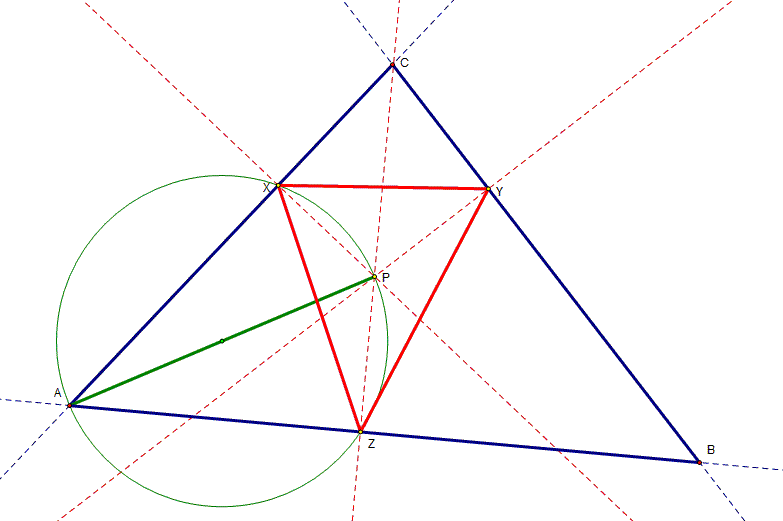
Let C be the circle
with AP as a diameter. Since both angle PXA and angle PZA are right angles and both subtend AP, points X and Z lie on circle C. Since both angle PAZ and angle PXZ are on C and subtend the segment PZ, angle PAB = PXZ. |
|
Step 2 Now I am going to prove that the pedal AíBíCí is
similar to ABC triangle. |
|
|
|
Let
Also letting So
The procedure is the
same for the other angles. So, for criteria AAA triangle AíBíCí is similar to
triangle ABC |
|
Note: All figures on this web page were made with The Geometerís
Sketchpad |