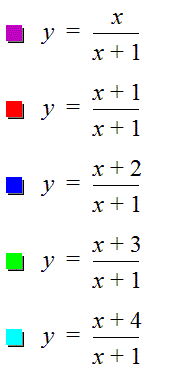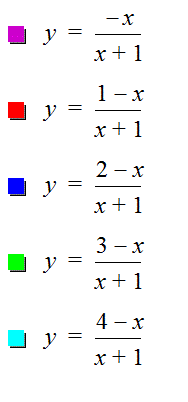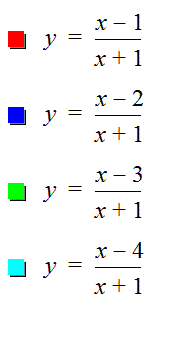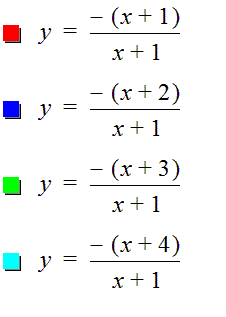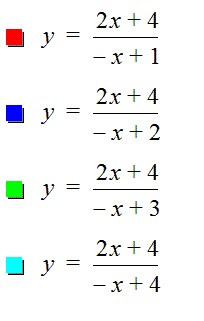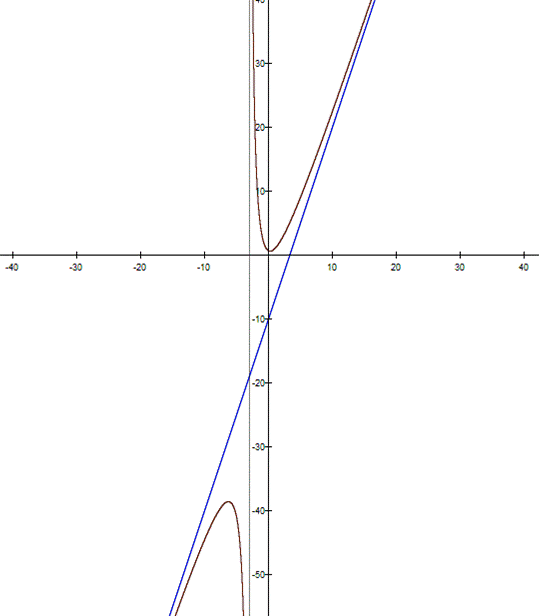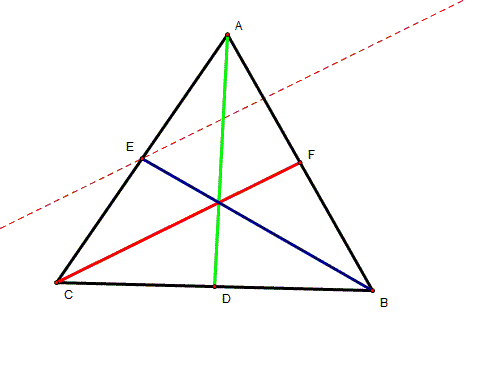---

Rayen Antillanca. Final Project

---

Part 1

Consider rational equations of the form . Explore the mathematical ideas for various values of the parameter a, b, c, and d.

Investigation 1

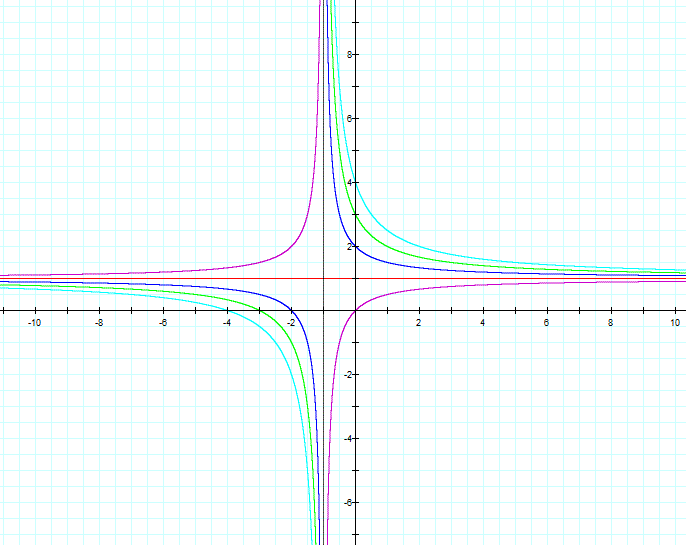
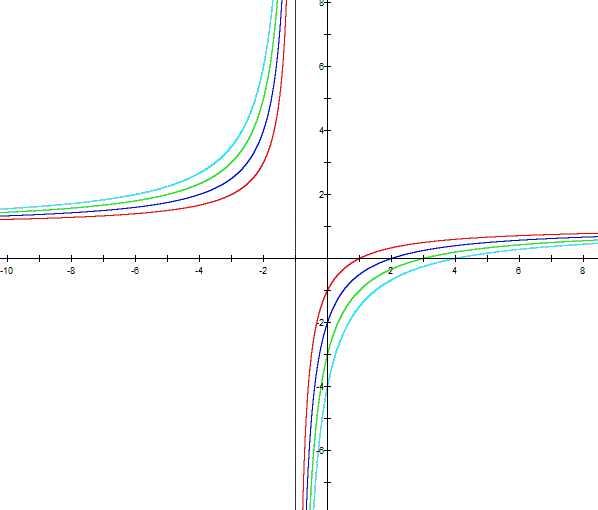
Consider the equation where a=c=d=1 and b>0 varies

Consider where a=-1, c=d=1 and b>0 varies
	The hyperbolas cut the y-axis in the value of b and the vertical asymptote is given by d, because the denominator is x+b. In this figure, the equation of the vertical asymptote is x=-1.

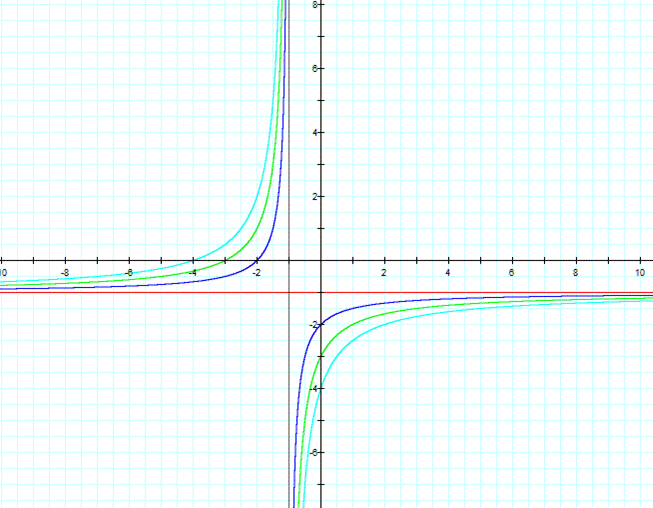
Consider the equation where a=c=d=1 and b <0 varies
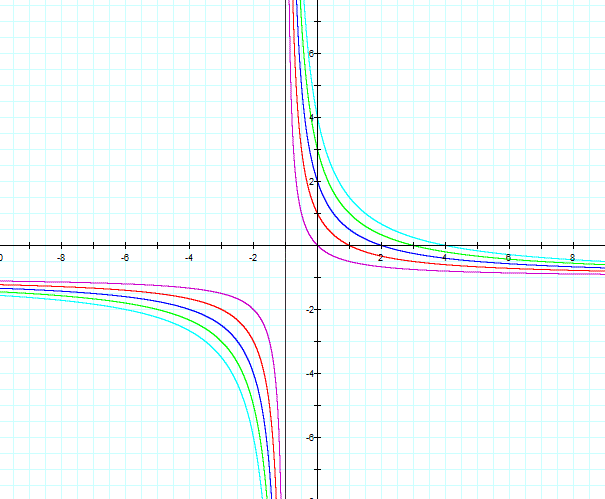
	As b is a negative number, the hyperbolas are in second and fourth quadrant. The value of d gives the vertival asymptote. In these equations the vertical asymptote is given by the equation x= -1.

Consider the equation where a=-1, c=d=1 and b <0 varies

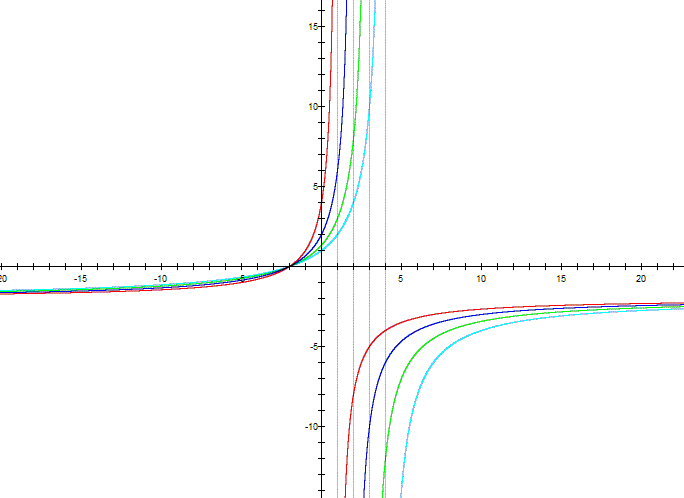
Consider a=2, b=4, c=-1 and d varies
	As d varies, the value of the vertical asymptote changes

Summary

, then if I take the numerator as a independent equation I get that , so , in this point is where the hyperbola cuts the x-axe.

Now, if I take the denominator as another independent equation,

, then, will be the vertical asymptote of this rational fraction.

Investigation 2

---

Now I am going to analyze what happen when where is a quadratic equation and is a linear equation.

Graph of
Let and As a rational equation as I can rewrite, after doing the division of polynomials, as The graph of this rational equation is the brown curve, which is a hyperbola. The blue line is the equation of which correspond to one asymptote of the hyperbola. And the other asymptote is which is given by the denominator of the rational equation, namely .

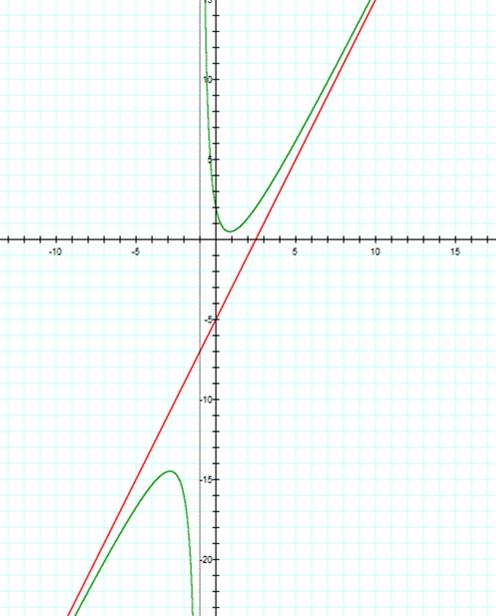
Another graph for
Let and . The rational equation, , after doing the division of polynomials I get: The green curve corresponds to the rational equation which is a hyperbola. The red line is one asymptote of the hyperbola which is given by the equation , and the other asymptote is , which is given by the denominator of the rational equation, namely
Summary In general, if , where is a quadratic equation and is a linear equation. We can rewrite this rational equation as the division of these equations. Where, is the quotient of the division and R is the reminder of the division. Then the asymptotes of the hyperbola will be given by and

---

Part 2

Square Inscribed in a Semicircle: Find a ratio

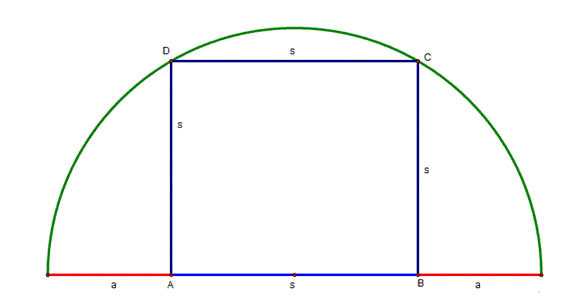
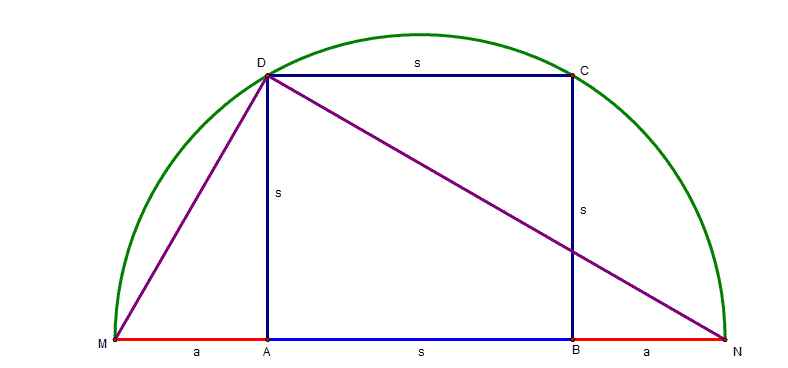
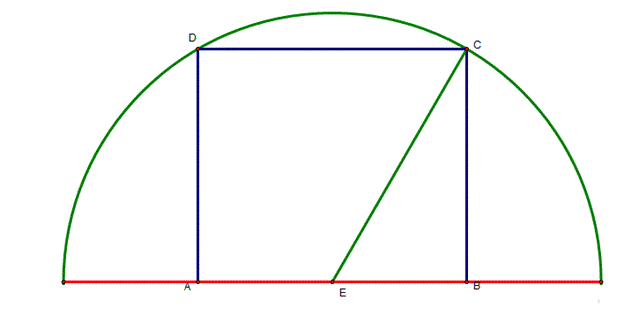
Given a semicircle with an inscribed square of side . Let be the length on the diameter on each side of the square. Find

Consider the triangle AND right in D because it is incribed in a semicircle. The triangle MAD right in A since AD is high. We can easily see that triangle MAD is similar to triangle AND, so that we may write the following proportion

(1)

Let , and replace in (1)

. Multiplying by x

rewriting as a quadratic equation

Solving this quadratic equation

The positive value of x solves this equation, because x is distance, which always must be positive, then

So I find the answer, which is , the Golden Ratio

Construct the square inscribed in a semicircle

Construction

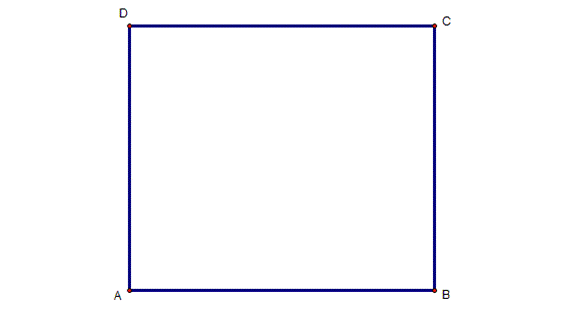
First, let ABCD any square

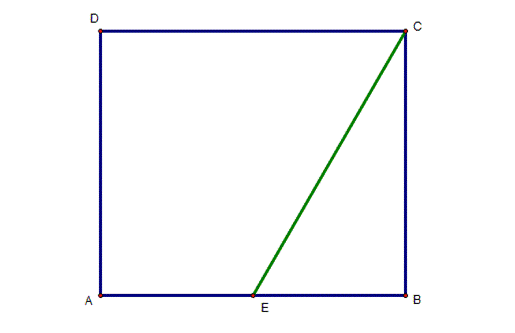
Draw a segment from E, the midpoint of AB, to C

Draw a semicircle with radius EC

Then, the square is inside the semicircle.

---

Part 3

Construct a triangle and its medians.

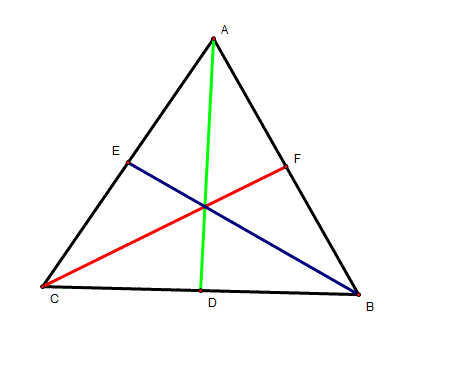
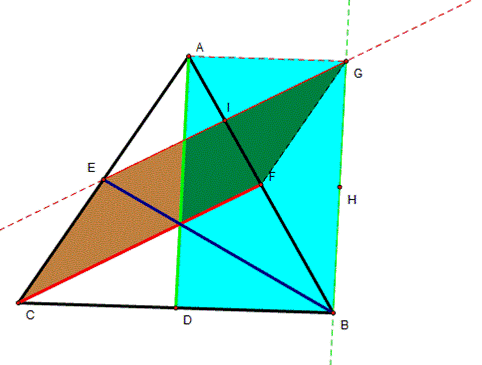
Let ABC be any triangle, where AD, BE and CF are medians

.

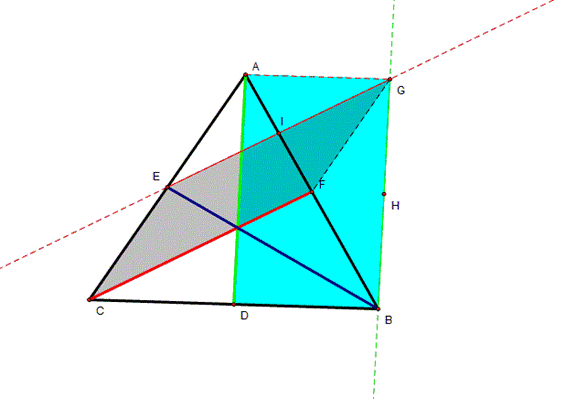
To construct a new triangle with the medians of triangle ABC
Construct a parallel line to a median CF that passes through point E.	Construct another parallel line to the median AD that passes through point B. Let G be the intersect point between these parallel lines.

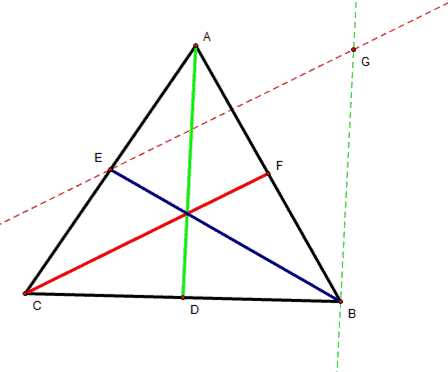
The triangle BEG is the triangle constructed by the three medians of the triangle ABC

Summary

The triangles ABC and BEG are not congruent, their sides are not equal according to the criteria SSS.

What happens with their areas?

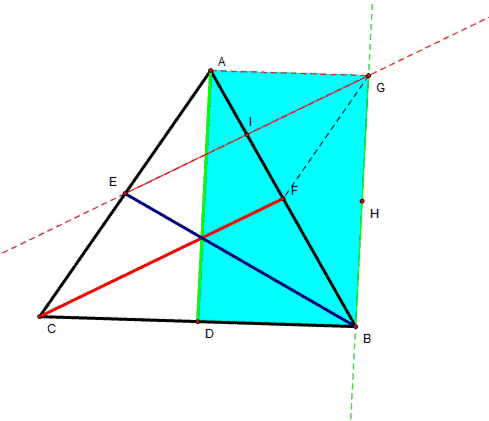
Notice this time we have two pairs of parallel lines, GF is parallel to EB and GC is parallel to AD. This created two parallelograms, FBEG and AGCD

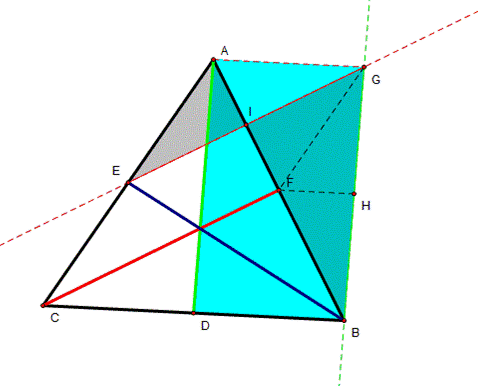
We know that the median AD of triangle ABC bisects the area of ABC in half. This means that Area triangle ADB is (area triangle ABC). Side AB is the diagonal of parallelogram AGBD, this means that triangle ADB is half the area of the parallelogram. Thus Area triangle ADB = Area parallelogram AGBD	We know triangle AIE is congruent to triangle FIG by ADA since EI = IG, by the midpoint theorem, angle AIE = angle FIG by opposite angles and angle AEI = angle FGI by alternate interior angles (AC is parallel to GF).

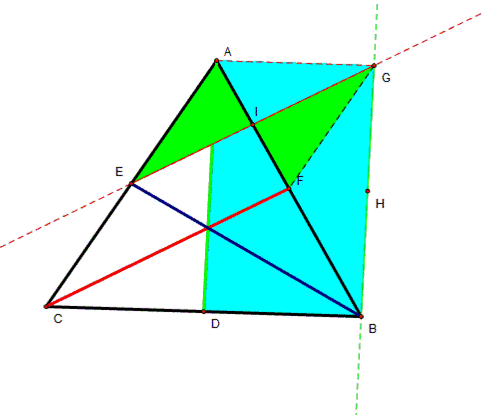
This gives parallelogram FGEC to have the same area as triangle ACF. Triangle ACF is half the area of triangle ABC so the smaller parallelogram is half the area of the larger parallelogram and half the area of triangle ABC.	Area of triangle AIE = Area triangle GIF = Area triangle AIG = Area triangle GFH = Area triangle BHF. Triangle GIB is half the area of the triangle made up of the medians and it has the same area as triangle GIF + triangle GFH + triangle FHC.

Summary

Triangle AGB has the same area as triangle AGI + triangle GIB. The area of triangle AGB = area of triangle ADB because they area each half of the area of Parallelogram AGBD. Since triangle ADB is half the area of the original triangle and triangle GIB is half the area of the triangle of the medians, we can use this to show that the triangle made up of the medians has an area that of the original triangle. Triangle GIB is of triangle AGB since it is made up of 3 of the 4 triangles with the same area. Since triangle AGB = triangle ADB then triangle GIB is the area of triangle ADB. Since triangle GIB is half the area of triangle GEB and triangle ADB is half the area of triangle ABC, then triangle GEB is the area of triangle ABC.

Note: All graphs of this webpage were made with Graphing Calculator 4.0 and the geometric images were made with The Geometer’s Sketchpad

Rayen's Homepage