EMT 668 - ASSIGNMENT 12, #6
The Spreadsheet in Mathematics Explorations

by

Kimberly N. Bennekin

Explore problems of maximization such as the lidless box formed from a 5x8 sheet with a square removed from each corner.

We want to create a box from a 5x8 sheet of paper by cutting out the corners and folding up the sides. Consider the following diagrams.

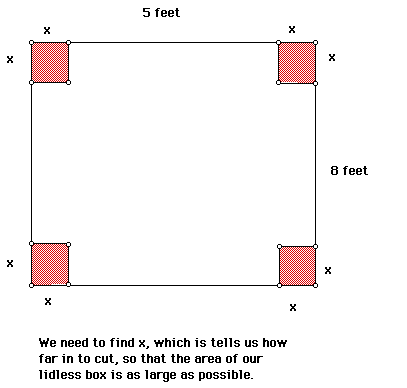
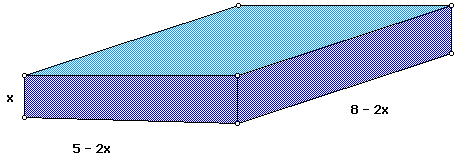
When taking 2x units from each side, the dimensions of our box are the following:

The volume of a box V is found by the following formula:

V = (length)(width)(height)

Thus,

V = (8 - 2x)(5 - 2x)(x).

We want to maximize this equation. We can see when this equation is maximized by looking at various values for x. We know that in order for our equation to make any sense, x only exists within the interval (0, 2.5), otherwise volume will be negative. Consider the following table:


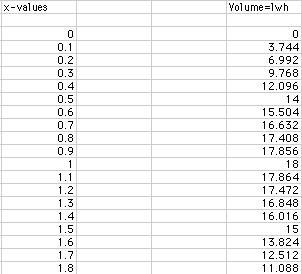
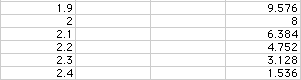
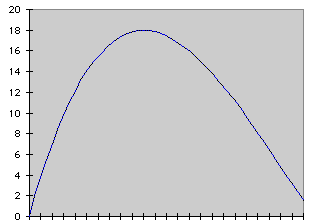
According to the table, a value of x = 1 will maximize the volume of the box. If we take a look at the graph of these values we can easily see that the maximum volume of the box is 18.


Return to Class Page