EMT 668 - ASSIGNMENT 8
Altitudes and Orthocenters

by

Kimberly N. Bennekin

1) Construct a triangle ABC with its Orthocenter H. Construct the triangles HBC, HAB, and HAC along with their Orthocenters as well.

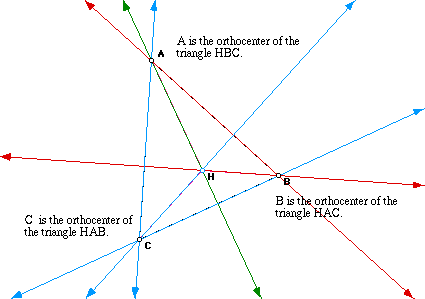
Each Orthocenter of HAB, HAC and HBC is also a vertex of the triangle ABC.

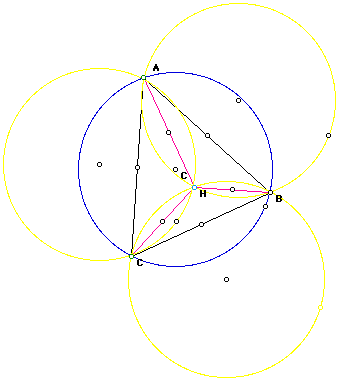
2) Construct the Circumcircles of the triangles ABC, HBC, HAB, and HAC.

Note that each Circumcircle intersects another object only at a vertex of the triangle ABC or at the Orthocenter of that triangle.

3) Construct the nine point circles for the triangles ABC, HBC, HAC and HAB.
Consider the Centroid of ABC as well.

The center of the nine point circle is the midpoint of the line segment connecting the Orthocenter to the Circumcenter.

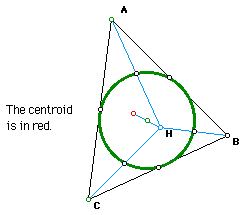
The nine point circle for all triangles is the same circle (in green). The Centroid is collinear with the Orthocenter and the Circumcenter. This line of collinearity is named the Euler line, after the renowned Swiss mathematician Leonard Euler who studied the properties of the nine point circle.

Return to Class Page