Quadratic Equation and its Coefficients by Jiyoon Chun
What does b do?
When we see the quadratic function y=
, we all know that how a, b, c affect the graph. I think c will be the easiest one to figure out because it moves the graph vertically. The next is a, because it affect whether the graph would be concave up or down. Then, how about b? We know that it affects the position of the graph somehow, but we did not try hard to investigate how the graph changes when b varies for fixed a and c.
To see how be affects to , let =0 and solve this equation for b.
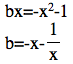where x≠0.
Now, x is independent variable and b is dependent variable. Therefore, we can graph the curve above in xb-plane.
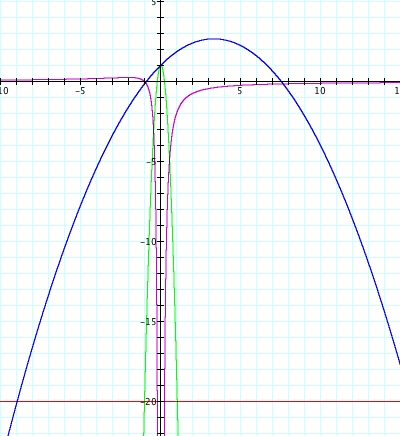
In this graph, when b=2 or -2, the graph meet at a point. When -2<b<2, there is no intersection. When b>2 or b<-2, then the curve and the line intersect at two point. Since this is xb-plane, x-coordinate is x value, i.e., the roots to the equation. Thus, coordinate of the intersection of b line and the curve tells directly about the roots according to b.
I would like to compare this curve to y=.
As we see in the flash above, the x-intercepts of the graph which is the roots of the given quadratic equation are all positive or all negative if they exist. When we draw b line on the xb plane, the intersections are either all positive or all negative. xb plane graph is useful to show when does exactly the roots to the equation exist, and their value. In xy plane, we also can see when we have solutions, but xb plane gives us clearer visualization.
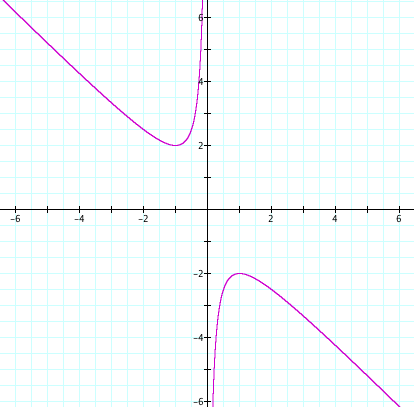
Suppose b=3. See the graphs below.
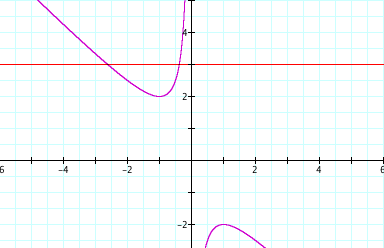
b=3 the curve intersect at two point. The x-coordinates are the root of the equation =0. We can see that we have two roots, and they are both negative.
What if b is not just a number such as b=kx?
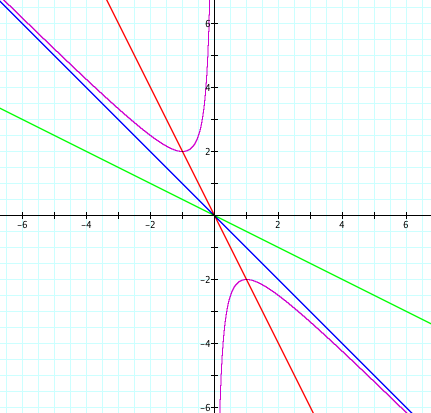
1) k>0 : No solution
When k>0, b=kx is on the 1st and 3rd quadrant. Since 
is on either the 2nd and 4th quadrant, there is no intersection.
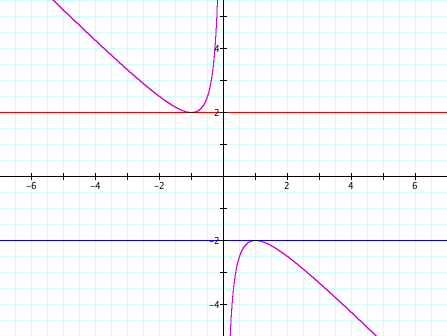
2) k<-1 : two solutions
In the picture above, the blue line is b=-x, and the red line is b=-0.5x. We see that b=-x and x=0 are the asymptotes of . Thus, there are two distinct root when k<-1.
3) k=-1 or k>0 : no solution
Actually this include k>0 case. SInce we do not have an intersection, there is no root.
In algebraically, we can see why this is the case.
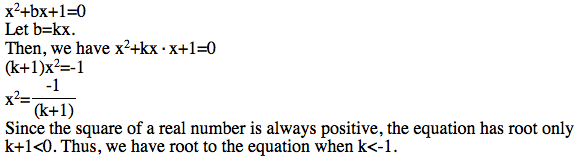
Example: b=-2x
As we see on the picture above, the roots are 1 and -1. Let's show it.
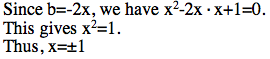
cx plane
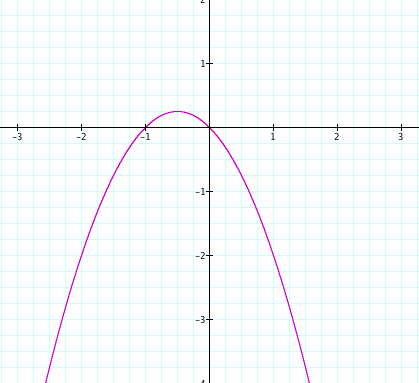
This can show the relation between a parabola and the line. We learned that the solution of two equation implies the intersection of two curves. In addition, the horizontal line means c=k, k is a real number. Thus, we have no solution when c>0.25, one solution when c=0.25, two different solution when c<0.25. The solution is x-coordinate of the intersection point.
ax plane
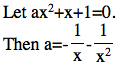
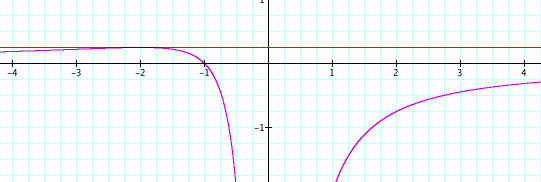
It is the same thing.
a=0.25, one solution
a<0.25, two solutions
a>0.25, no solution.
Well, however, this does not say anything about shape of the graph, y=
, whether it is concave down or concave up. However, it gives idea about how narrow the graph is going to be. See the picture below.
This is when a=-1.5.
We see the distance of two solution is perry far compare to what appears in the next picture.
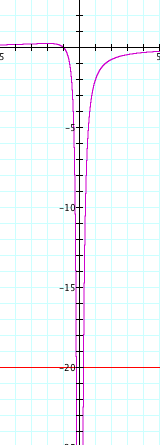
When a=-20, the distance between the two solutions are pretty close. Thus, we can naively say that the graph will be narrower when a=-20 than a=-0.15. See the picture below.
