Jiyoon Chun
Centroid
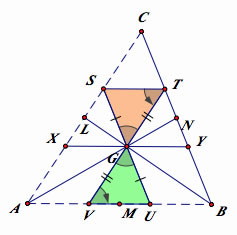
The concurrency of the three medians
-Do they really intersect at a single point?
Idea of the proof
Since median from a vertex to an opposite side divide any parallel segment of the side into two equidistant pieces, show that the centroid is the midpoint of XY.
Proof
Let G is the intersection of two medians AN and BL.
Construct SU parallel to BC crossing G and TV parallel to CA Crossing G.
Since AN is a median, SG=GU.
With the same reason, TG=GV.
In addition, ∠TGS=∠VGU.
Thus, △GST≈△GUV.
By the property of the congruent triangles, ∠STG=∠GVU.
Thus, by Euclidean parallel axioms, ST∥ VU .
Therefore, ST∥AB.
Let XY be parallel to AB.
Since ST∥AB, ST∥XY.
Now, SGYT is a parallelogram. Thus, ST=GY.
SXGT is also a parallelogram. Thus, ST=XG.
Since G is a midpoint of XY, the median from C and G intersects at G since a median cut any parallel segment to an opposite side in half.
Centroid is (2/3)of the distance from a vertex to the midpoint of the opposite side.

∠LNA=∠BAN and ∠BLN=∠LBA since AB∥LN.
∠LGM=∠BGA.
Thus, △LNG≈△BGA.
LN=(1/2)AB because L and M are the midpoint of CA and BC respectably.
Therefore, GA=2GN .
If we show this works for other similar triangles, we can easily show that centroid is (2/3)of the distance from a vertex to the midpoint of the opposite side.
The area of six little triangles
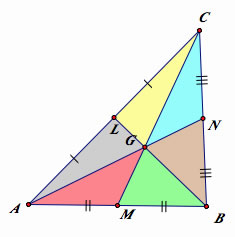
The idea of the proof:
When the base and the height is the same, the area of the triangles are the same.
Question?
Why the area of the triangles of the same height and base are the same?
Answer:
To figure this out, we first have to analyze the meaning of the area formula.
The area of the triangle=(1/2)*base*height.
"base*height" is the area of the rectangle. Thus, it means that the area of a triangle is the half of the rectangle of the same base and height. This makes sense when the triangle is a right triangle.
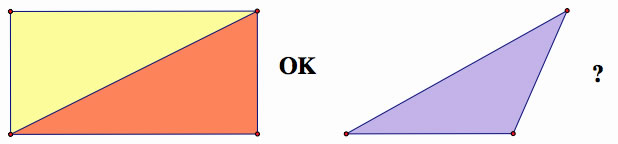
If we construct parallel lines of two sides of a triangle, then we have a parallelogram.
As we see in the picture, we can get the area of a parallelogram by cutting and pasting a part of it.
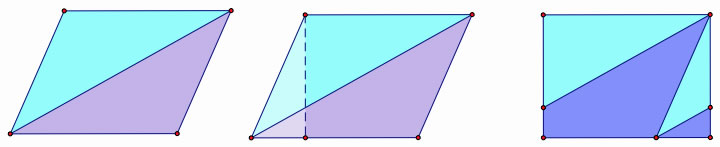
Then what if cutting once is not enough to refrom a rectangle?
Like this!
the area of ABEF= the area of ABCD
AF=EB, ∠F=∠E, FD=EC since AB=DC by the property of parallelogram.
Thus, △FAD≅△EBC.
the area of FABC-the area△FAD=the area of FABC-the area△EBC
Thus, the area of ABEF= the area of ABCD.
Therefore, the area of the rectangle and the parallelogram of the same base and the height are the same.
The area of six little triangles
Let the area of △ABC=1.
Then, the area of △CMB is (1/2) △ABC since M is a midpoint of AB.
Now, the area of △CGB=(1/3)△CMB because g is the (2/3) distance of the vertex. Thus, △GMB=(1/3)△CMB=(1/3)*(1/2) △ABC=(1/6).
This gives △CGB=(1/3) since △CGB=△CMB-△GMB=(1/2)-(1/6)
In addition, △CNG=△NBG since they have the same base and share height.
Therefore, △CNG=(1/2)△CGB=(1/2)*(1/3)=(1/6)=△NBG.
In the same sense, △CLG=△LGA=△GMA=△GMB=△NBG=△CNG=(1/6)△ABC
Show that the concurrency of the medians is a special case of Ceva's Theorem
Ceva's Theorem

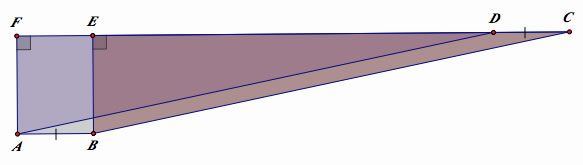
Given △ABC with an arbitrary point P. Segments AD, BE, and CF are constructed through P to the intersection with the opposite side.
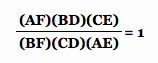
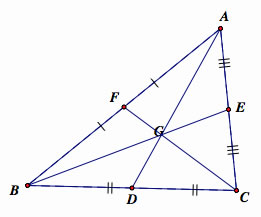
Since G is the intersection of three medians, AF=BF, BD=CD, and AE=CE.
Therefore, e intersection of three medians, AF=BF, BD=CD, and AE=CE.
Therefore, 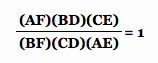 .
.
In the case of quadrilaterals
Two different centers
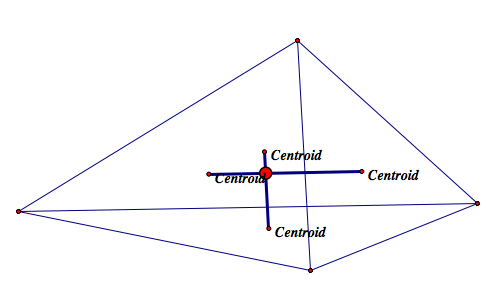
There are three centers of a quadrilateral depends on where we put on. The first one is the intersection of the two diagonal. The second one is the intersection of two segments which connect the centriod of the half of the quadrilateral (four triangles forming a quadrilateral). The third one is the intersection of the two medians.
Then what is the centriod of an quadrilateral?
I think we have to know what is the definition of the centriod, and differentiate the definition case by cases.
Center of vertices
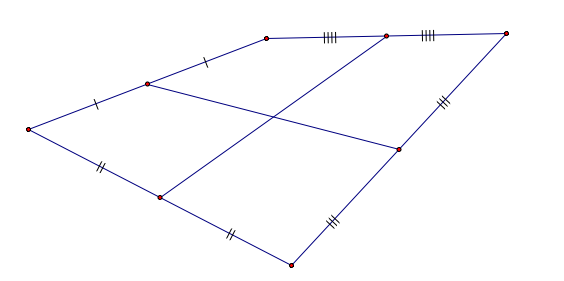
If we see there are unit weight on the each vertex, then the center of the quadrilateral is the intersection of the medians.
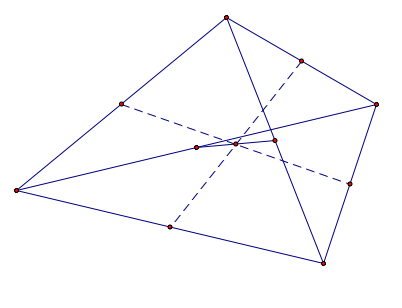
The point is also the midpoint of the segment which connects the midpoints of the diagonals. The proof is easy and I will leave it for the readers.
Center of area

If we see a quadrilateral as a thin piece of four sides, then the center of area is the the point where we can valance a quadrilateral. Thus, if we break the quadrilateral into two triangles and find the centroid of each, the center of mass of the quadrilateral is on the segment connecting the two centroids. If we break up the quadrilateral two different ways, we get two such segments. The intersection is the center of mass of the region.
By the definition of the centroid, any line which divide the quadrilateal into two equal area must hit the center of the area.
