Parabola by Jiyoon Chun
Parabola
A parabola is the set of points equidistant from a line, called the directrix, and a fixed point,called the focus. Assume the focus is not on the line. Construct a parabola given a fixed point for the focus and a line (segment) for the directrix.
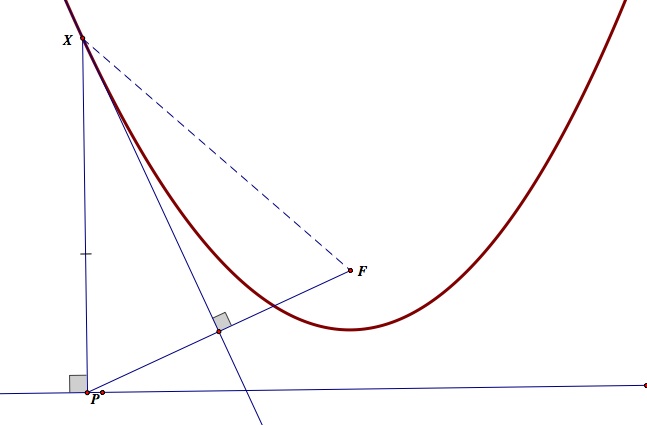
The locus is the trace of X which satisfies XF=XP for given f and a point on the given line L.
How to construct:
STEP 1: Connect F and P.
STEP 2: FInd the midpoint of PF and construct a perpendicular line to PF on the midpoint of PF.
STEP 3: Construct a perpendicular line from P on L. This will indicate the distance between X and the line L by the definition of the distance of a point and a line.
STEP 4: By the property of an isosceles triangle, we have XF=XP, and the trace is parabola.
Proof by coordinate geometry:
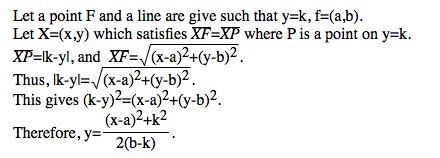
Question: What if the denominator is 0?
Here, we noticed that k≠b since it make the denominator 0.
Geometrically in means that the focal point cannot be on the given line because it simply makes the distance between the focal point and a point on the line 0.
Or we also can see the mid point from a focal point on the directrix and a point on a directrix is just the directrix. However, I think it is meaningful to see why.
In fact, if we move the focal point toward the given line (directrix), we can see the width of the parabola getting narrower and narrower and eventually it disappears (see the video clip below).
Thus, we can conclude that the distance between a focal point and a directrix affects the width of the parabola. It makes sense because we know that the bigger than leading coefficient is, the narrower curve we get. However, I think it is important to figure it out why geometrically.
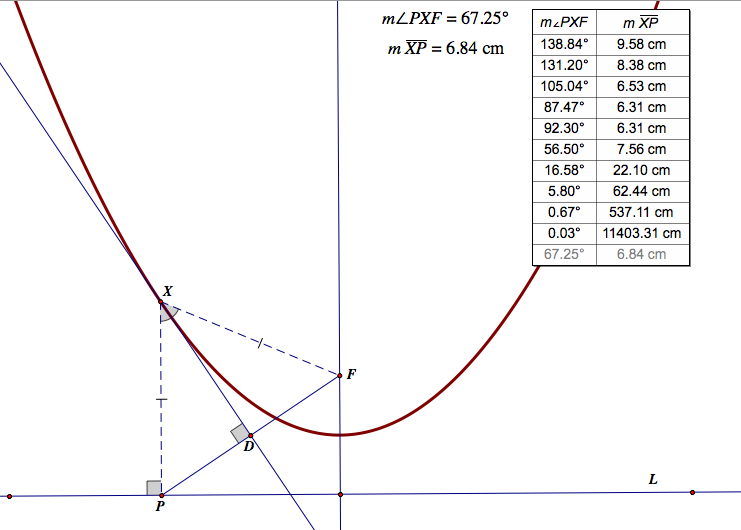
As we see the video and the picture above, we can observe why the distance between the focal point and the directrix affects the width of the parabola.
I think the shape od the triangle PXY is the reason why we have different curve. The parabola is the trace of X which is the top point of the isosceles triangle. When F approaches to a directrix, triangle PXF becomes acute triangle. the top point X locates really high when the triangle is acute. I think this is why we have narrow curve. When f is far from the directrix, we have obtuse triangle which x locates comparably low. I do not think this will be the exact answer since the length of FP is not fixed when F is moving. However, it will be meaningful activity for the students to think and developed the concept of the parabola.
Trace of the Tangent Line
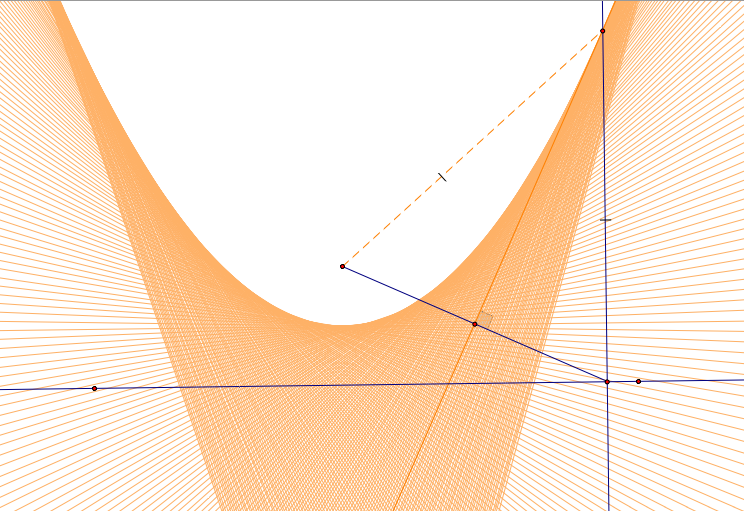
When the directrix is a circle
It is interesting when the directrix is a circle. First, let's just watch the video clip below.
It seems like we have three different curve and a point; Hyperbola, ellipse, circle, and a point.
Ellipse
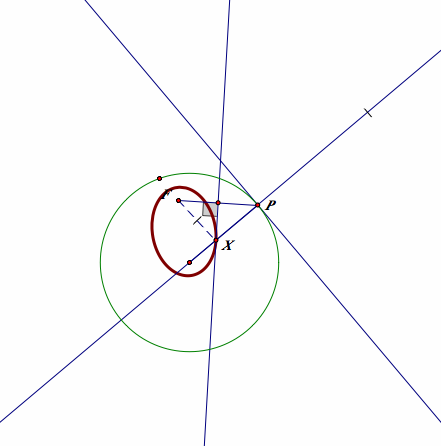
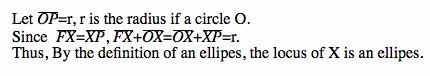
Hyperbola
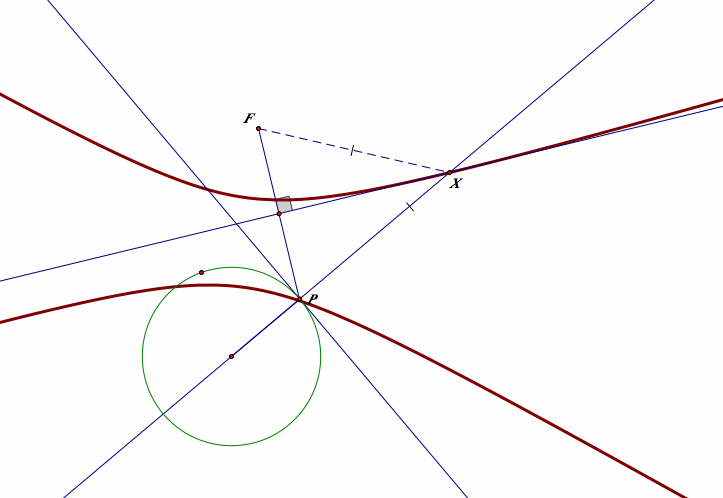
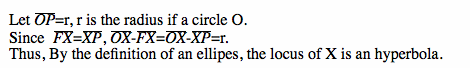
Simply on the given circle
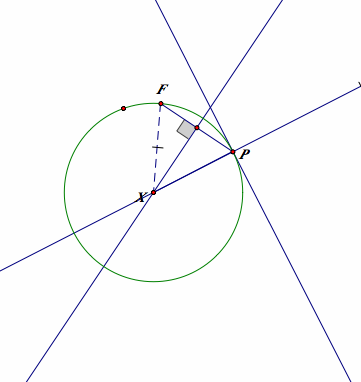
This is pretty simple. what happens when the focus on the directrix?
Then, there exists unique point X which is equidistant to F and P. It is a center.
Therefore, the locus is a point, the center of the given circle.
When the focus is the center of the given circle
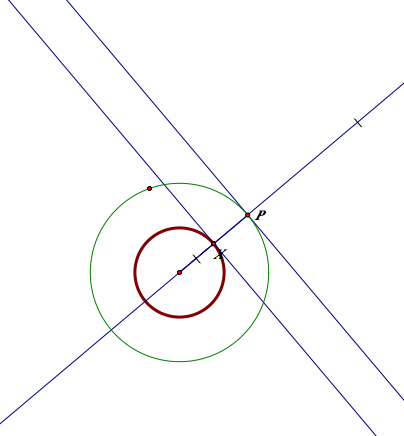
This is simple, too.
When the focus is the center of the given circle, the equidistant point from the focus and a point on the given circle is just a midpoint of them. Therefore, the locus if the circle of the same center and half of the radius of the given circle.
