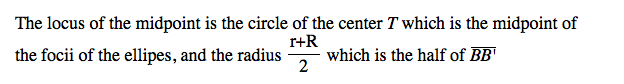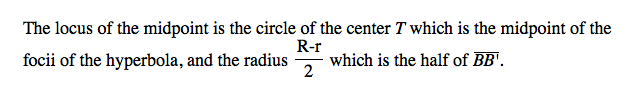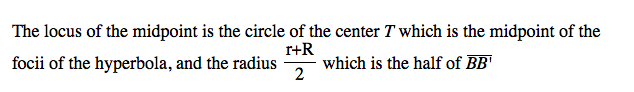Tangent Circles by Jiyoon Chun
I will investigate inner and outer tangent circle when two circles are given
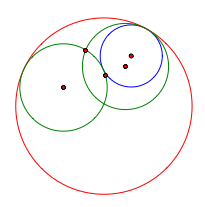
We have three different situations.
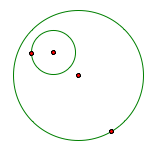
1. A circle is inside of the other |
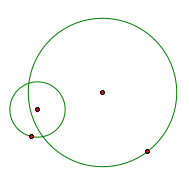
2. Intersect |
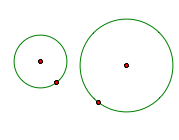
3. Separate |
 |
 |
 |
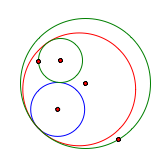
Our goal is constructing two tangent circles as below! |
||
 |
 |
 |
As we see in the table above, we have two tangent circles; The blue and the red one.
If you want to play with this, here is the custom tool of this!
We will investigate the locus of the center, and also the midpoint which is essential to construct the tangent circle.
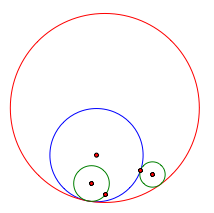
1-1 When a circle is inside the other circle
-The blue tangent circle which is tangent outside of the little circle which is inside of the big given circle, and inside the big given circle.


1-2 When a circle is inside the other circle
-The red tangent circle which is tangent outside of the little circle which is inside of the big given circle, and inside the big given circle.


Observation
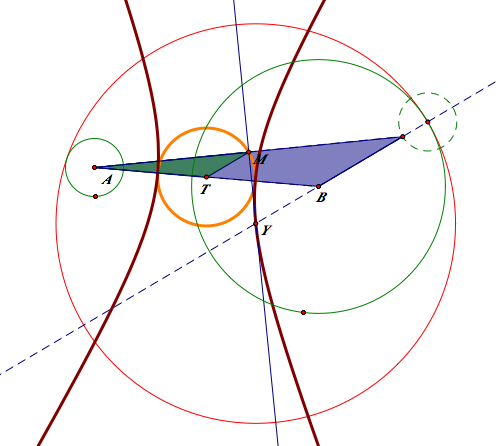
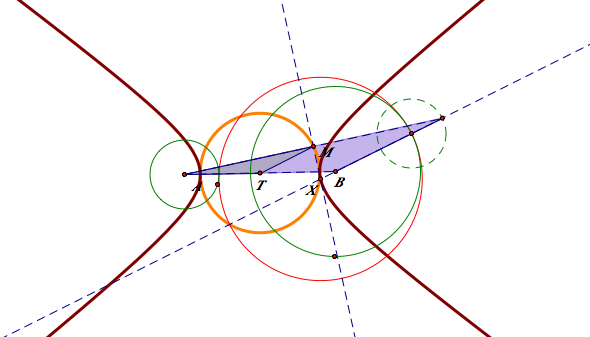
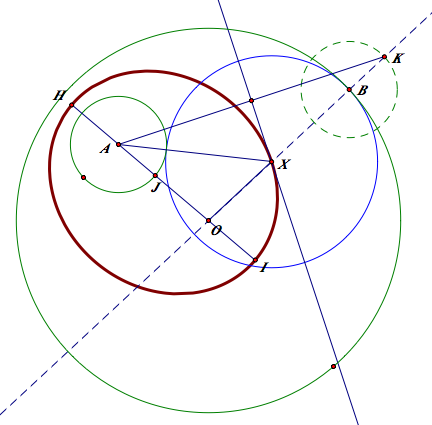
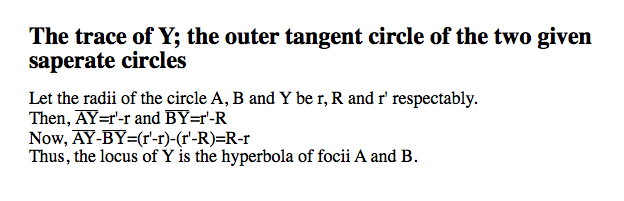
When we construct eh blue tangent circle, we added the radius little circle on a point on the big circle. On the contrast, we subtracted the radius of the little circle on a point on the big given circle. Since two green circles are given, the radii of the two circles constant. Therefore, when we add the distance from the center of the tangent circle to each center of the given circles, the radius of the tangent circle which varies cancels out. By the definition of the ellipse, we know that the locus will be the ellipse In addition, we can easily predict the length of the major axis while we construct the tangent circle. For the blue tangent circle, we have r+R since we added the little circle. For the red one, r-R for the same reason.
Since the constructions of the tangent circles are pretty much the same, I will omit the construction, and focus on the locus of the centers.
2-1 When the circles intersect
-The blue tangent circle which is tangent inside and outside of the given circles.

2-2 When the circles intersect
-The red tangent circle which is tangent inside and outside of the given circles.

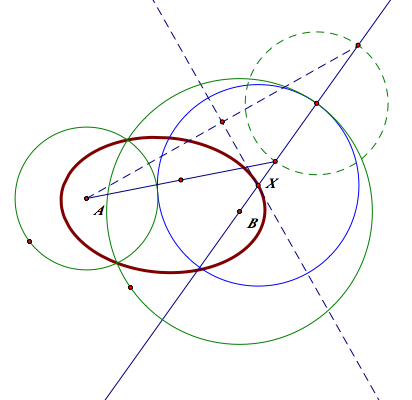
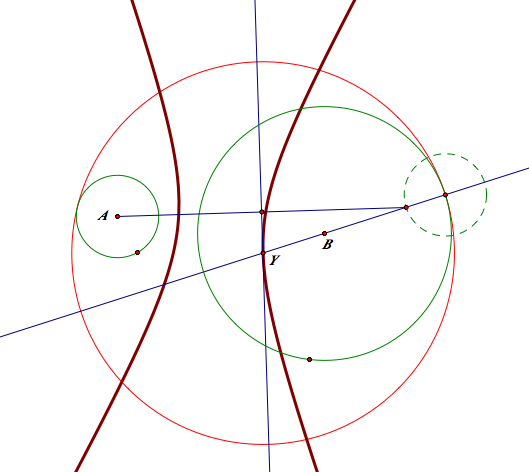
3-1 When the circles are separate
-The blue tangent circle
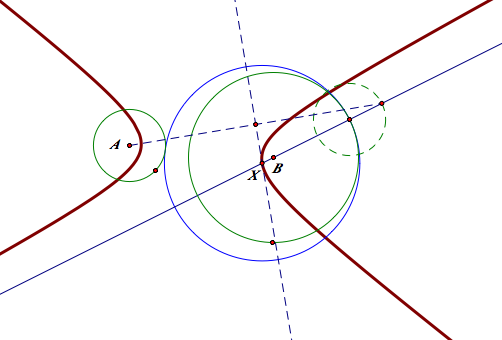
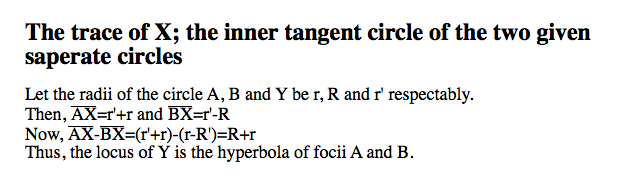
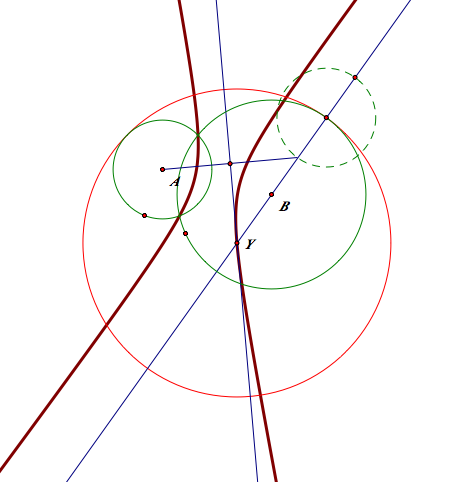
3-2 When the circles are separate
-The red tangent circle
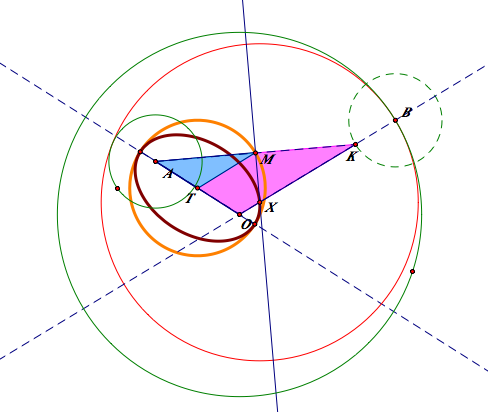
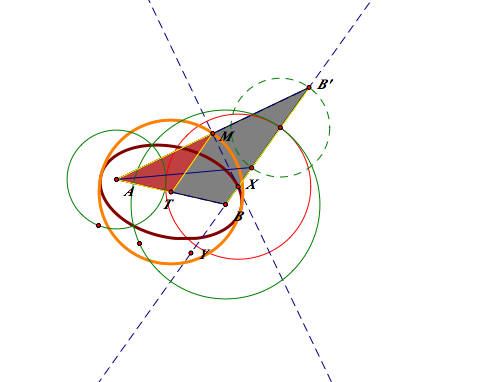
The role of an isosceles triangle
The role of an isosceles triangle is critical here, because it enable us to find the equidistant point of the two given point. To create the isosceles triangle, we have to get the mid point of the two given point.
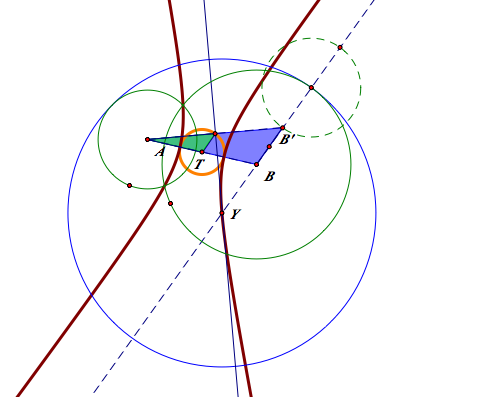
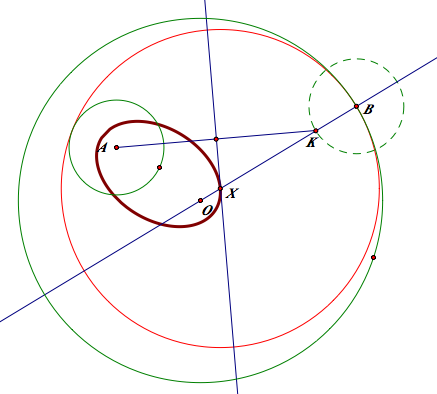
The trace of the midpoint of the isosceles triangle
In case of 1-1
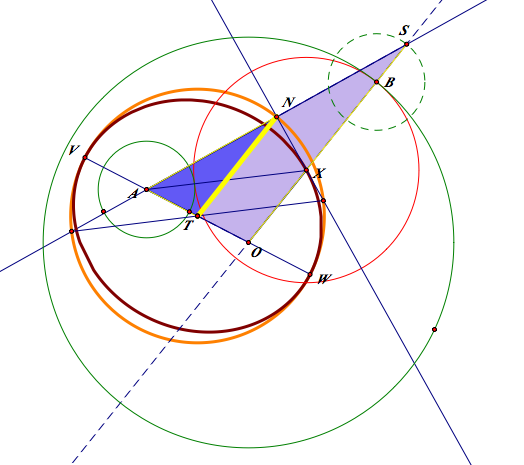

The trace of the midpoint of the isosceles triangle
In case of 1-2