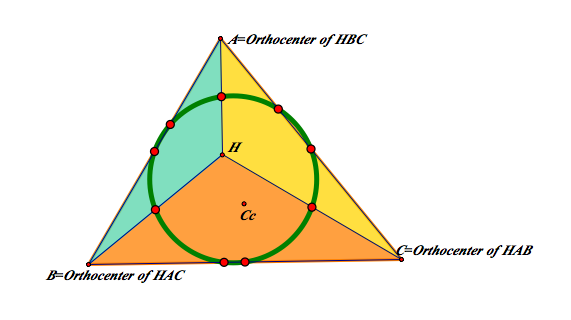
Nine Point Circle by Jiyoon Chun

---

What is a nine-point circle?

---

Every triangle has orthocenter,and a midpoint of each side.

There are three midpoints of the three sides of a triangle.

There are three prependicular feet from three vertices to opposite sides.

If we connect the orthocenter to each vertex, we can get three midpoints of the segments.

Now, we have nine points, and they are all on the same circle.

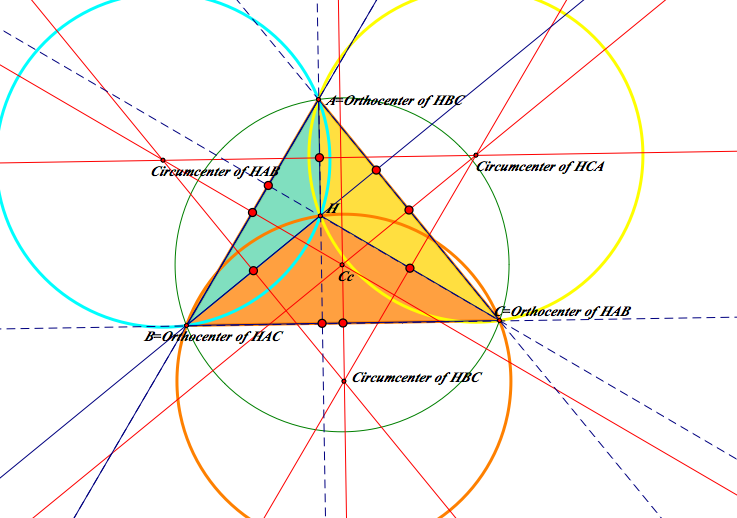
I marked the nine points big, and it seems like they are on the same circle. Let's proove it.

---

Before the proof- the property of a rectangle and the circumscribed circle of the rectangle

---

There is one key property that I will use all the time to prove the existence of the nine point circle.

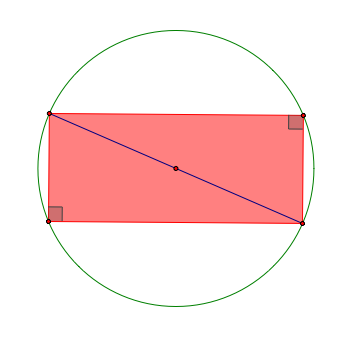
Since the sum of the diagonal angles is 180°, we can always construct a circumscibed circle of a rectangle of which the center is the midpoint of the diagonal by the property of the inscribed angles of a circle.

---

STEP 1: Finding a rectangle

---

---

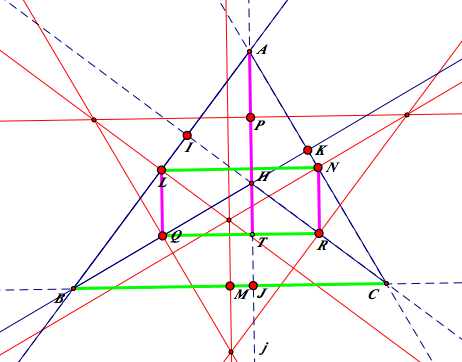
STEP 2: Constructing a circumcircle

---

---

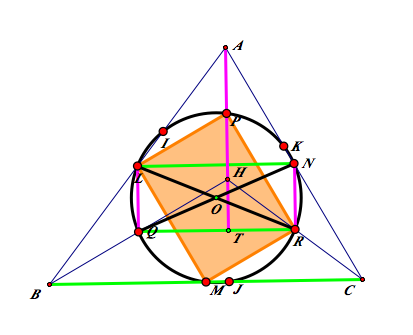
STEP 3: Finding other rectangle which share the diagonal

---

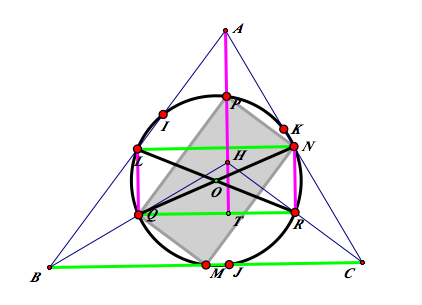
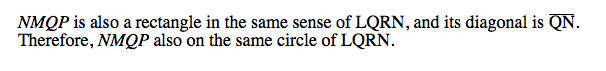
We proved that all the midpoints of △ABC, and the midpoints from H to A, B, C are on the same circle.

Let's prove all the perpendicular feet to A, B, and C which are I, J K, are also on the same circle by the property of the inscribed angle of a circle.

 

---

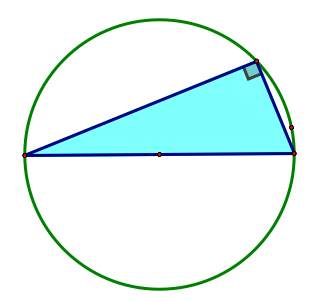
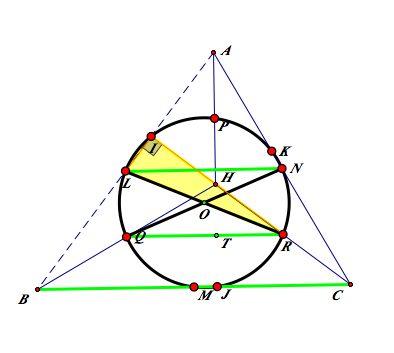
One more property- When does the inscribed angle become a right angle?

---

We know that the opposite angle of the hypotenuse is 90° when the triangle is inscribed in a circle and the hypotenuse is the diameter of the circumscribed circle. Like the picture below.

---

STEP 4: Finde the inscribed right angle of the same diagonal

---

---

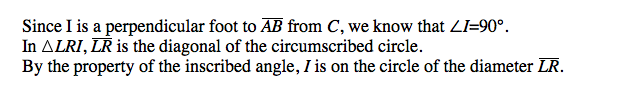
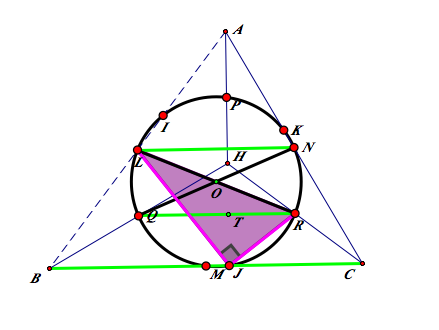
In the same sense, J is on the same circle.

---

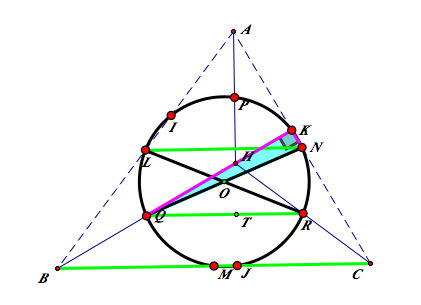
In the same sense, K is on the same circle.

Now, we have all nine points on the same circle!