Similarity of Pedal Triangles by Jiyoon Chun
What is the pedal triangle?
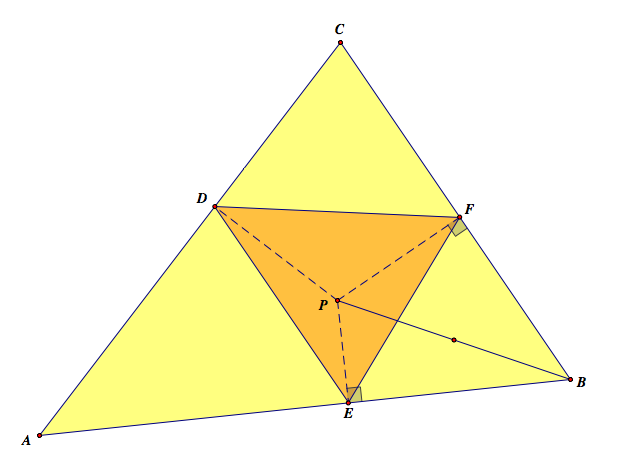
Let P be any point on a plane, and ABC be a triangle. If we put perpendicular foot to the each side (if the side is not big enough, we can extend it), we have three intersection points. Let those point be DEF. Then, the pedal triangle of ABC is the triangle DEF.

When P is inside of ABC
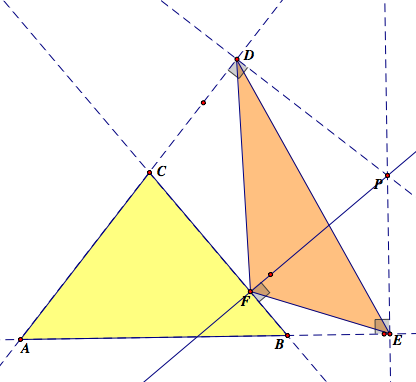
When P is outside of ABC
Similarity of the pedal triangle
The pedal triangle of the pedal triangle of the pedal triangle of ABC is similar to the triangle ABC. In the picture below, the purple triangle is similar to the triangle ABC.
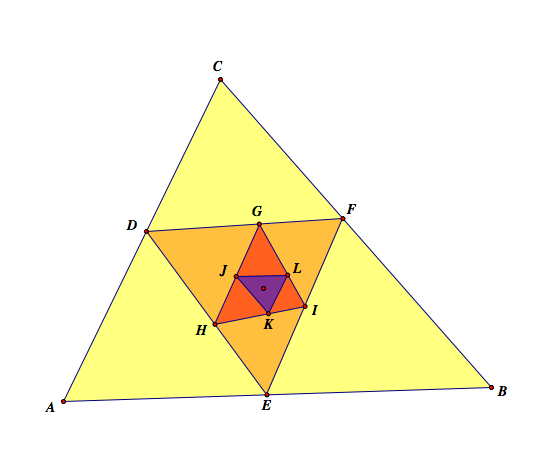
Intuitively, there must be some kind of relation between the triangle ABC and the pedal triangle of ABC since the pedal triangle is consists of three perpendicular lines to the sides of the triangle ABC. However, it is really interesting why the third pedal triangle is similar to the given triangle ABC.
Before the proof
There is two things that I want to use to prove the similarity of the pedal triangle.The first one is the property of the inscribed angle. As we know, the measure of the inscribed angle stays as long as they are based on the same arc.
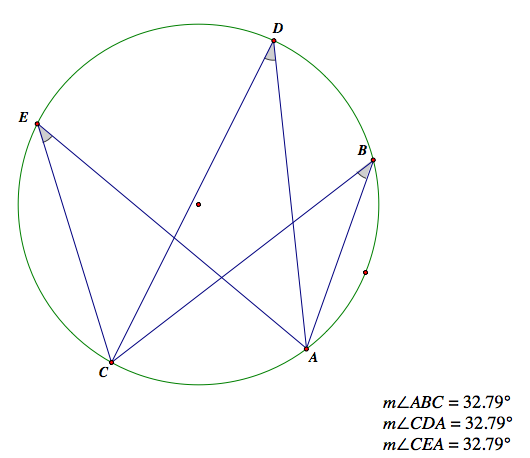
As we see the picture above, the angle B, D, and E are congruent because they all share the same arc AC. WHY?
Property 1: The relationship between the central angle and the inscribed angle
As we see the video clip below, the measure of the central angle is the double of the inscribed angle.
Let's prove it.
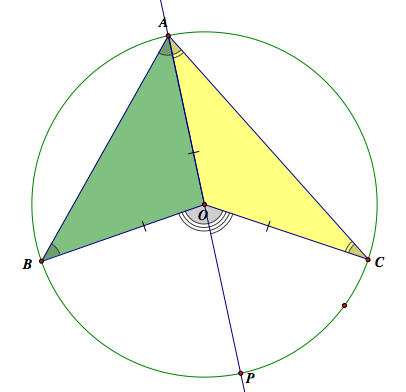
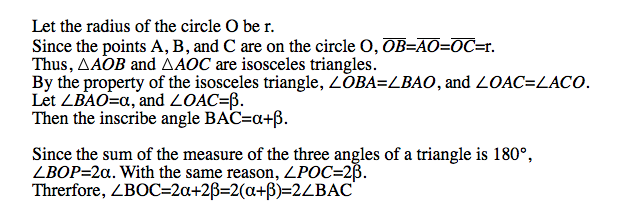
When the arc is fixed, the central angle is fixed, too. Thus, the inscribe angle should be constant since the measure of the inscribed angle is always the half of the central angle.
Property 2: the Circumcircle of a quadrilateral
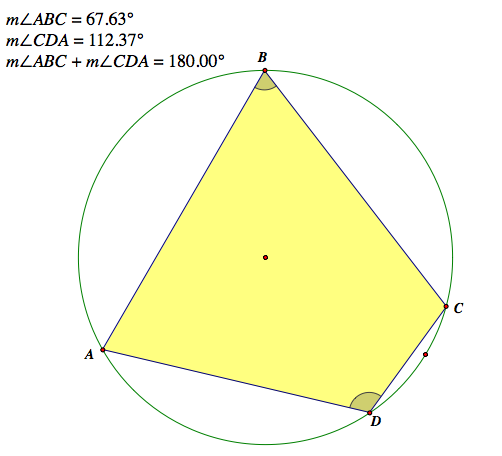
As we see the picture above, the sum of the opposite inscribe angles is 180°.
Thus, if the sum of the opposite angles of a rectangle is 180°, we can construct the circumcircle of it. The reason is pretty simple. Since the central angle of the whole circle is obviously 360°. Therefore, the inscribed angle of the whole circle is 180°.Since the angle B is based on the arc AC, and the angle D is based on the arc CA (counterclockwise), the sum of the angle B and D should be 180° because the sum of the arc AC and CA is the circumference.
Now, we are ready for the proof.

The pedal triangle gets smaller and smaller, and it is not easy to see it. So, I will show the relationship between the yellow and the orange triangles, then orange and red one, and red and the purple one. Eventually, I will show the similarity between the yellow triangle ABC and the purple triangle KLJ.
1. △ABC and △DEF (the yellow one and the orange one)
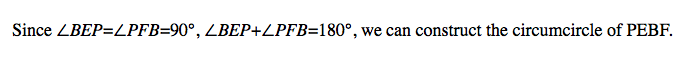
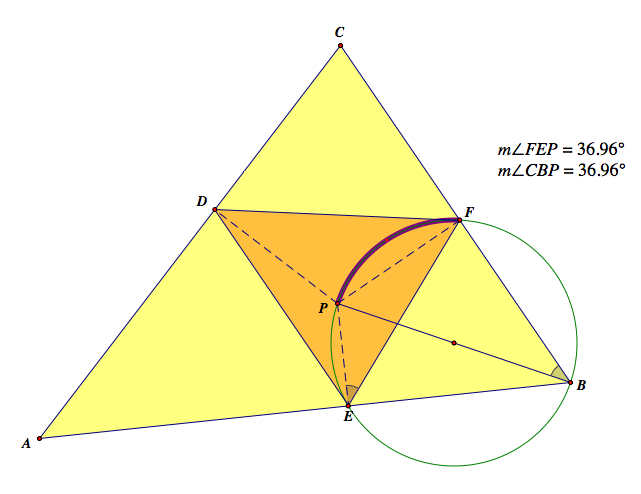
![]()
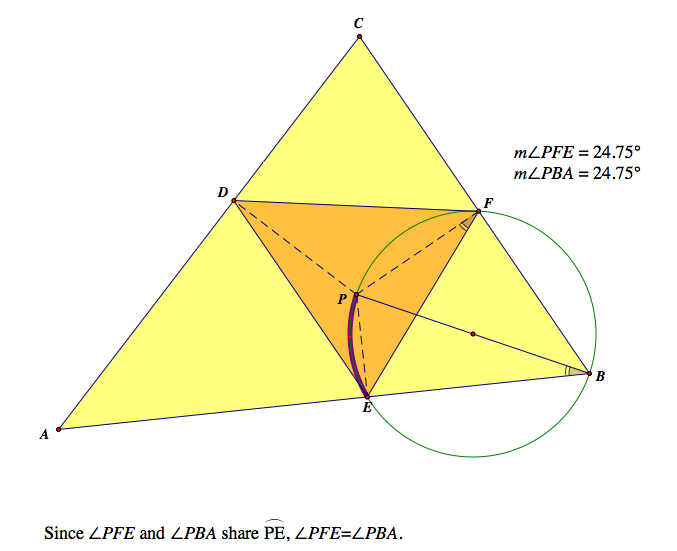
We can do the same job for the each angle C, and A.
In the picture below, we can see how the angles of ABC rearranged in the pedal triangle DEF.
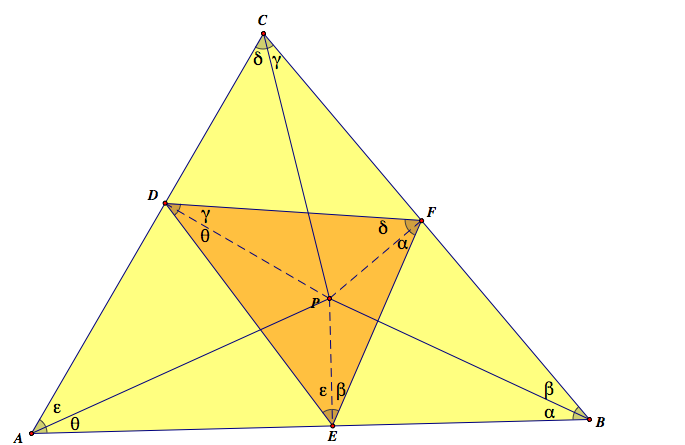
2. △DEF and △GHI (the orange one and the red one)
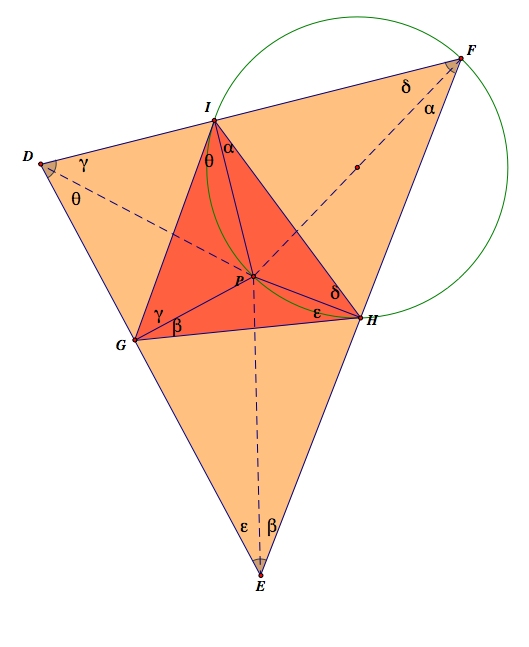
I drew only one circle of diameter PF. There are two more circles of diameter PD, and PE. We can easily see that which angle correspond to which angle.
3. △GHI and △JKL (The red triangle and the purple one)
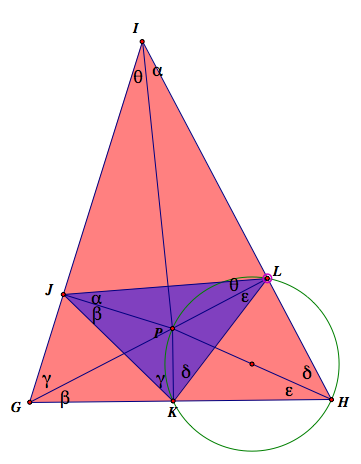
As we see above, ∠J=α+β, ∠K=γ+δ, ∠L=ε+θ in △KLJ.
4. Conclusion: △KLJ≈△CBA (The third pedal triangle is similar to the triangle given.)
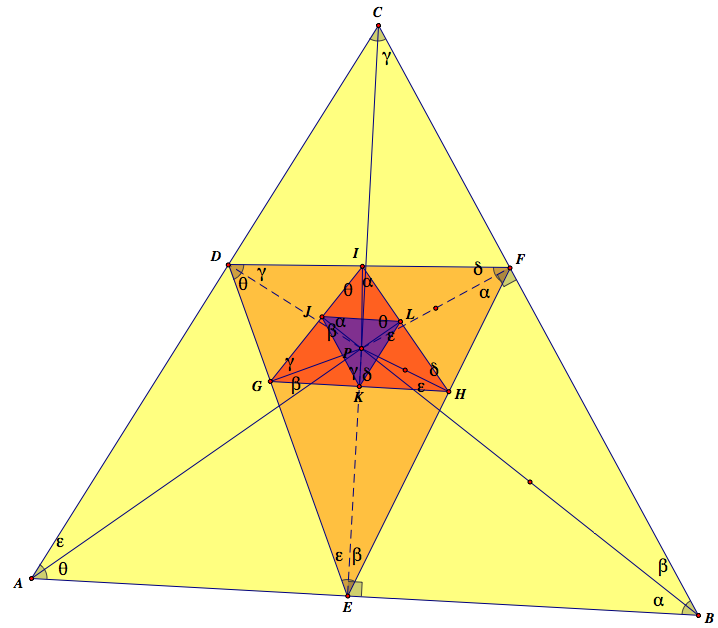
Here is the final picture of the three pedal triangles and △ABC.
Observation
Since all the angles (α,β,γ,δ,ε,θ) stays, I noticed that they are rotating under the certain law. Therefore, the rearrangement of the six angles can be a cyclic group. For the convenience, let's number the angle such that α=1,β=2,γ=3,δ=4,ε=5,θ=6.
Take a look at the picture below.
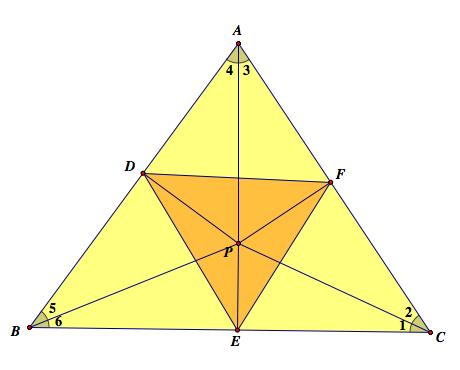
However, it is hard to decide which angle of △DEF should be correspond to which angle of △ABC. Well, as long as we make a certain rule, it really would not be a problem because the angles are rotating. Thus, let ∠D be the correspondent angle of ∠C, ∠A to ∠E, and ∠B to ∠F. It is just simply see the triangle upside down and mark all the angles counterclockwise.
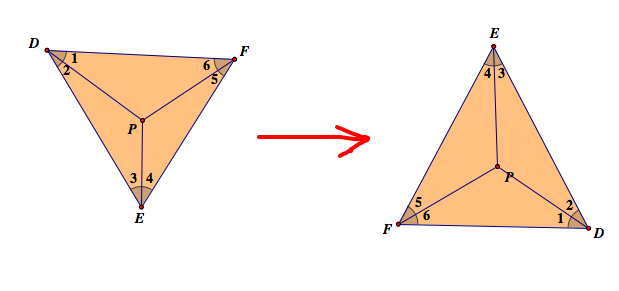
It is always confusing which goes which in the cyclic group. In the picture above, we know that ∠1 in △ABC=∠5 in △DFE. Thus, 1→5. In the same sense, ∠2 in △ABC=∠4 in △DFE. Thus, 2→4
∠3 in △ABC=∠1 in △DFE. Thus, 3→1
∠4 in △ABC=∠6 in △DFE. Thus, 4→6
∠5 in △ABC=∠3 in △DFE. Thus, 5→3
∠6 in △ABC=∠2 in △DFE. Thus, 6→2. In short,
1→5
5→3
3→1
2→4
4→6
6→2
Therefore, we have (153)(246).
Since the length of the cyclic group (153)(246) is 3, we know that the third pedal triangle will have the same angles with △ABC. In this way, we can figure it out why the third pedal triangle is similar to the given △ABC without constructing three pedal triangles.
