Tangent Circles of a Point on a Given Circle and a Given Line by Jiyoon Chun
How to construct a tangent circle of an arbitrary point P on a given circle to a given line?
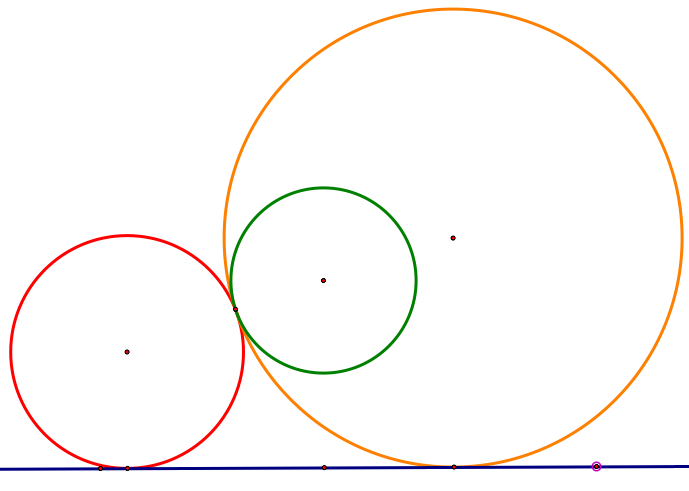
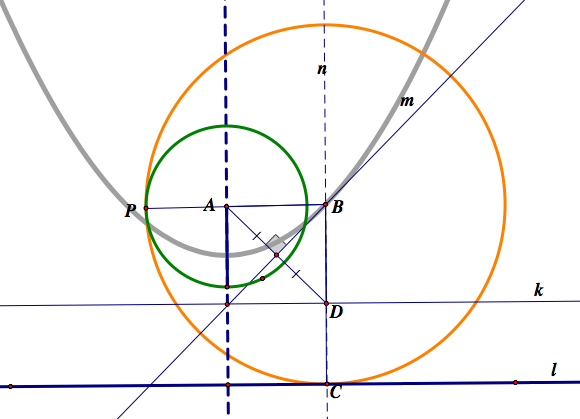
Let the green circle and the blue line given. For an arbitrary point P on the green circle, there exists two tangent circle: The red tangent circle which is tangent to the green circle outside, and the orange circle which the green circle is tangent to inside of the circle.
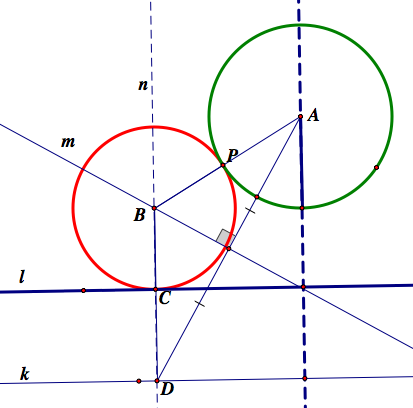
Construction and proof of the red tangent circle
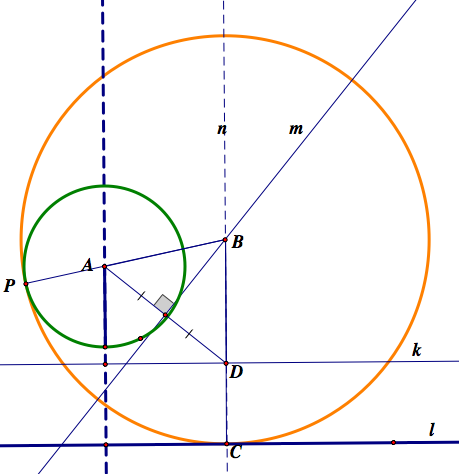
Construction and proof of the orange tangent circle
The locus of the tangent circles
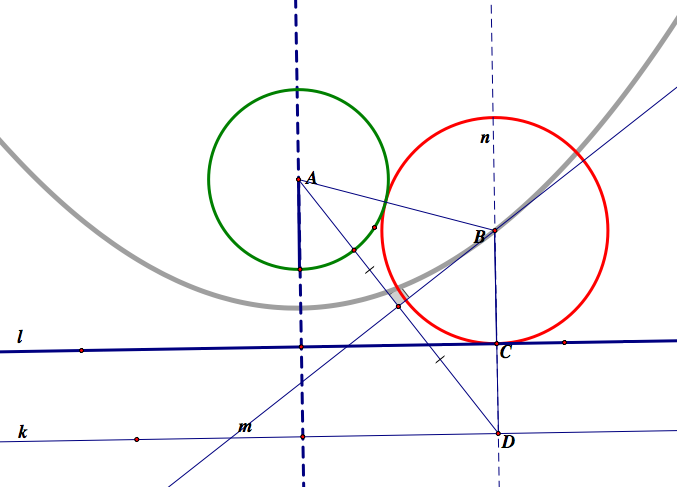
The locus of the center of the tangent circle is a parabola of a focal point A and directrix k. A is a center of a given circle, and k is the line parallel to given line l and distance between l and k is the radius of the given circle A.
What is the difference?
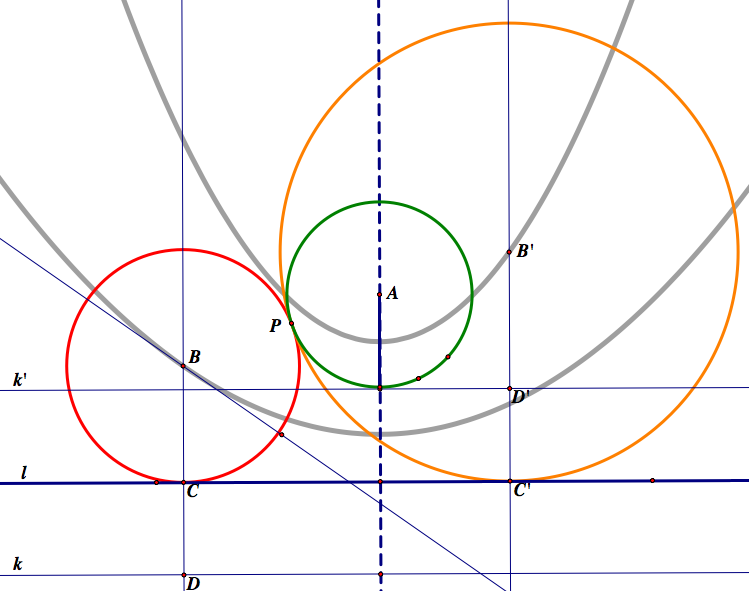
When we constructed circle B, we first drew the line k. Therefore, the locus of B is the parabola of the center A and directrix k.
WHen we constructed circle B', we first drew the line k'. Thus, the locus of B' is the parabola of the same center A and directrix k'.
Since k' is closer to the focal point A than k, the locus of B' is narrower than the locus of B.
The limiting case of tangent circles
Let's think about the radius of the tangent circle when point Dāā
1) the Red tangent circle
Intuitive thinking
As we can see in the flash above, the slope of AD converges to 0 when Dāā. Then AD will be parallel to AC. Since B is on line m which is perpendicular to AD, B also goes to infinity when D goes infinity. Thus, when P is on the intersection of circle A and perpendicular line to the given line l passing through the center of the given circle A, than we have a tangent circle of radius infinity. Thus, the tangent circle will be a tangent line at a point P. See the picture below.
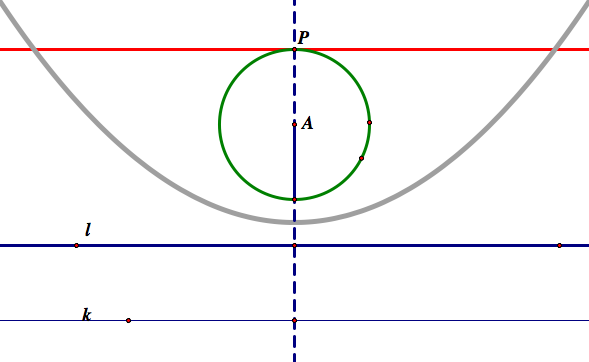
Algebraic proof
Suppose that A is at 
and 
. Then the locus of the center of tangent circles is 
. Thus, the coordinate of point B is 
. Since the tangent circle is tangent to the given circle A at point P, |PB| is the radius of B.
|PB|=
.
Since P is at 
, 
.
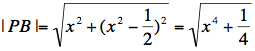See the flash below.
When I move the given circle so that point P is on the line given, we can observe that the radius of the red tangent circle is getting bigger and bigger and eventually it will be the line given. In addition, the line given is tangent to the circle given. The same intuitive thinking and algebraic proof can be applied to explain this.
2) the Orange tangent circle
As in the flash above, we can observe that the tangent circle becomes the line given when point D goes to infinity. Since the construction is the same, the same reasoning of the red tangent circle also explains why the tangent circle becomes the line given. I am attaching another flash.