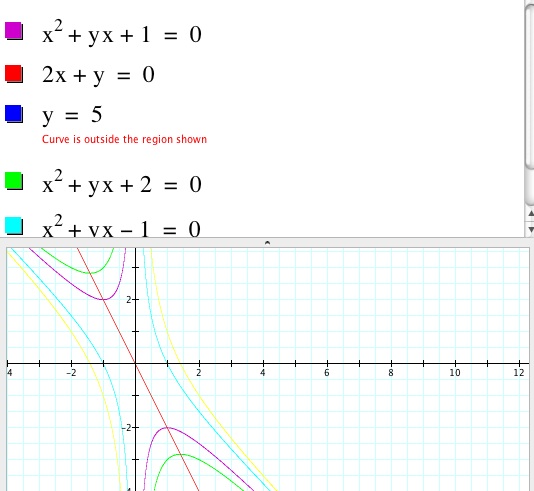
Assignment 3: Investigation 2
The purpose of this assignment is to explore the
distinguished characteristics of a hyperbola as well its inverse, in addition
to a linear function presented to intersect the hyperbolic function. It is
important to note that significant changes take place when the selected the
constant c is changed. This is also true when the original equation of the
Hyperbola exhibits its natural characteristics with the two curves directly
reflecting each other and the graph approaching the y-axis but never touching
it. The y-axis clearly serves as its asymptote.
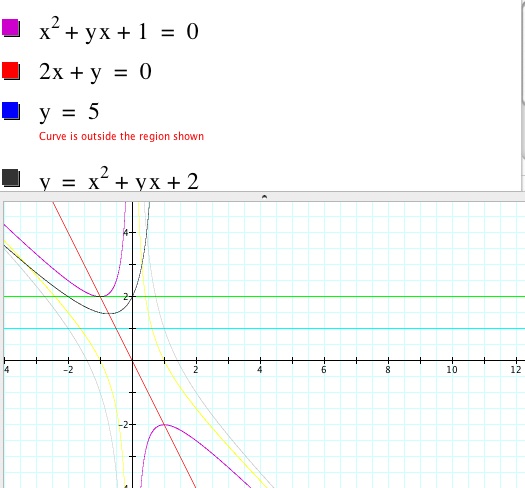
When the constant c is
negated to -1, the two curves not only shift positions, but completely change
the configuration. It appears to be to inverse of the original function. The
horizontal linear line with the slope of zero, intersecting the original
function yields two negative roots while yielding one positive and one negative
root on the inverse function. The
horizontal line will ultimately intersect the curve in the curve in the fourth
quadrant, where the roots of the original function will be positive at the
vertex.
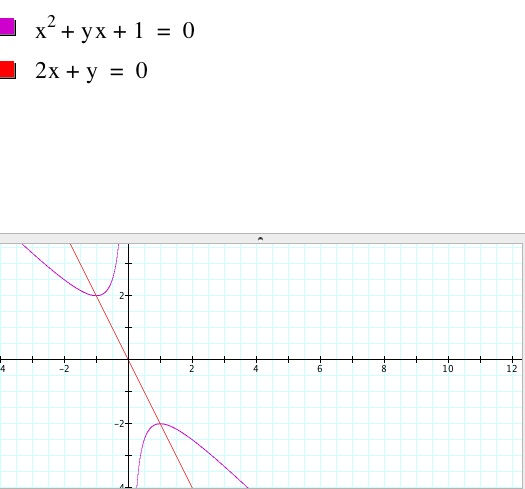
Under investigation 2, the same mathematical phenomenon
occurs as the original function and the second one are inverse functions of
each other as the constant c is negated. In addition, the new line, 2x +b =0,
with a negative slope of -2, now serves a line of reflection intersecting the
original function while it does not intersect the inverse function. The line
serves a line of symmetry as well on the inverse function.
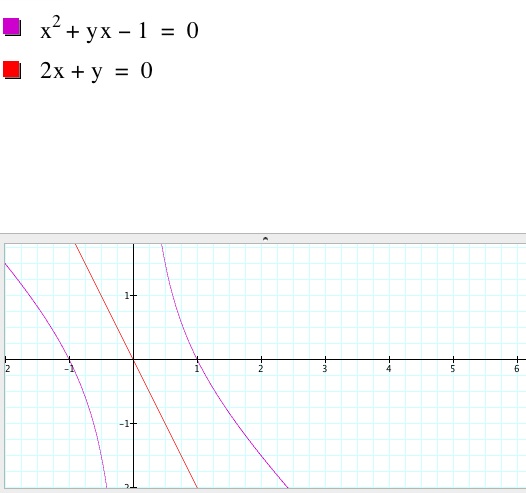
As the constant c
increases, the characteristic of the original hyperbolic function remains the
same yet stretching the curve. As the constant c is negated, the
characteristics of the inverse function also remain the same as the curve equally
stretches.

In the investigation, when the constant changes to n, the
hyperbolic function becomes a three dimensional figures where the lines become
two dimensional planes and the original functions become three dimensional
curves. One interesting discovery was when the equation is no longer expressed
as an equation and written as an expression, the graph becomes three
dimensional and the linear expression is a surface with an area.