Assignment 1 by Butila Kialeuka(Diekumpuna)

Exploring two linear functions through compositions.

The purpose of the assignment is to explore with different pairs of f(x) and g(x) along with their graphs in order to analyze the results of various operations including: addition, subtraction, multiplication and division of the two functions.

Set 1 y= f(x) = 2x + 1 y=g(x) = -3x – 5

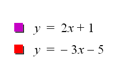
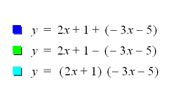
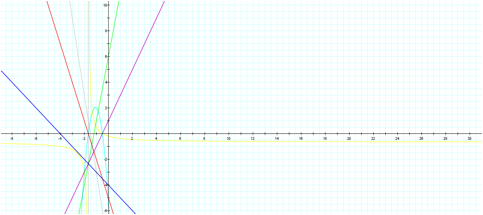
Analyzing the compositions of the above linear functions, each operation yields a different result respectively as the two equations have different slopes. When adding and subtracting the two linear functions, the result remains linear where as when multiplying or dividing the two functions, the result is completely different as expected. The product of the two linear functions results in a parabola as it becomes a quadratic functions. The quotient of the linear functions, on the other hand, results in a hyperbola. It is important to note that all of the compositions remain functions as they all pass the vertical test respectively. The composition of f(g(x)) will always yield a linear relation since the coefficient of f(x) is being multiplied to both addends of g(x ). When conducting the mathematics manually, the two functions resulted in linear functions as well in exception of when the two were being divided and multiplied. Product confirmed the graph and resulted into a parabola where as the quotient resulted into a hyperbola.

Set 2 y= f(x) = 2x + 1 y= g(x) = 2x -3

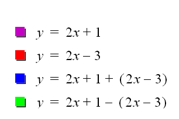
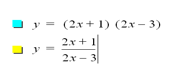
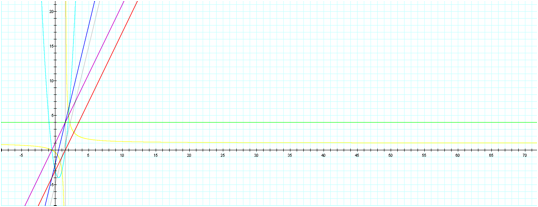
Using another pair of linear functions having the same slope, which are parallel lines, the same result was generated as it was in the first set of equations, in exception of when finding the difference of the two linear functions which yield a line with zero slope as the group of variables cancel each other out. These are still functions as the vertical line test was conducted to verify the validity of the function. The composition of f(g(x)) will always yield a linear relation since the coefficient of f(x) is being multiplied to both addends of g(x ). The manual manipulation of the mathematics resulted in responses support the graphical representations of the functions.

Set 3 y=f(x) = 2x + 1 y=g(x) = -x∕2 +4

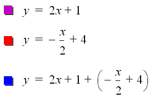
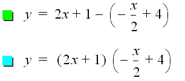
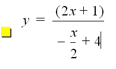
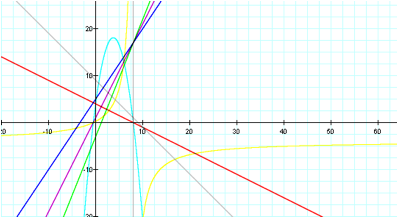
The third set involves the linear functions that are perpendicular (negative reciprocal of each other).Both the difference and sum of the composite intersect with the second function, g(x). The product of the two functions remains a parabola where as the quotient results in a hyperbola. All of the compositions remain functions as they are validated through the vertical line test. These assumptions can be made provided the x remains the independent variable. The composition of f(g(x)) will always yield a linear relation since the coefficient of f(x) is being multiplied to both addends of g(x ). The manual manipulation of the mathematics resulted in responses support the graphical representations of the functions.