

BY: ERICA FLETCHER
Graphs in the xb plane.
Consider the basic quadratic equation
![]()
where b is any real number.
Now graph this relation in the xb plane. We get the following graph. The graph below shows how the values of x and b relate to each other. The x values are along the x-axis and the b values are along the y-axis.
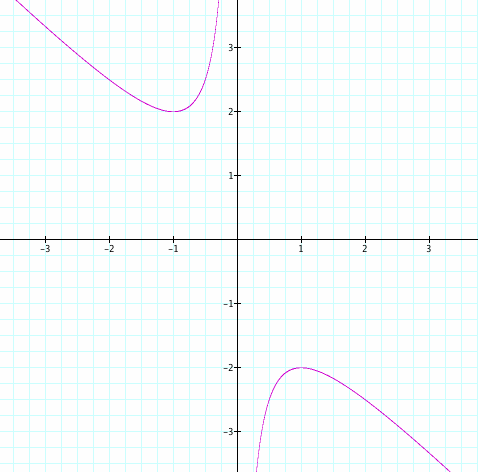
If we take any particular value of b, say b = 5, and overlay this equation on the graph we add a line parallel to the x-axis. If it intersects the curve in the xb plane the intersection points correspond to the roots of the original equation for that value of b. Therefore, we have the following graph.
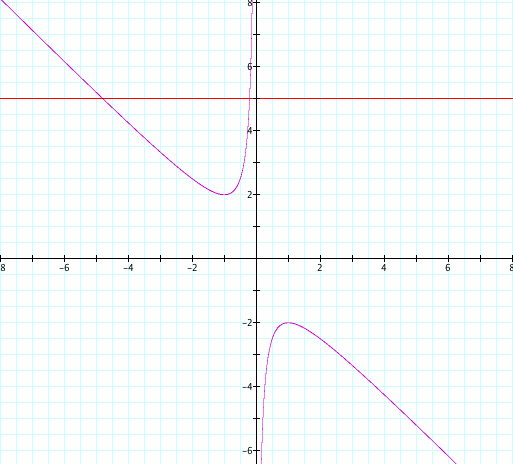
We notice below, for each value of b we select, we get a horizontal line.
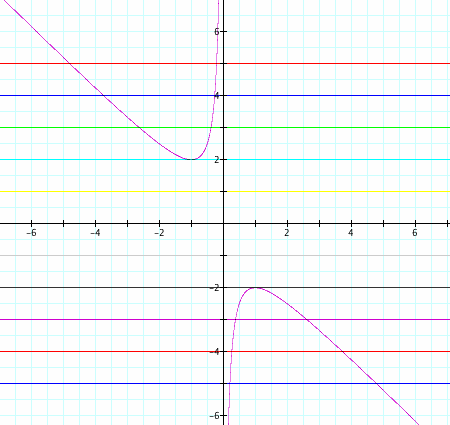
Notice the gap between the two sections of the graph. Between -2 < b < 2, there are no values for this graph. It is very clear on a single graph that we get two negative real roots of the original equation when b > 2, no real roots for -2 < b < 2, one positive real root when b = -2, and two positive real roots when b < -2.
Lastly, let's consider the case when c = -1 rather that +1.

Consider the following equation again:
![]()
where a = 1, b =1, and c = -1.
If we look at the discriminant now we see that the above graph makes sense because we will always get two roots.
Let's look at the discriminant:
![]()
Since c = -1 the discriminant will always be greater than zero.
Return to Fletcher's Home Page