


By: Erica Fletcher
The football rules in college football were changed a few years ago have made the uprights 5 feet narrower than previously. Many game commentators have harped about how much harder it is to kick field goals from the hash marks. Assume the field goal is attempted from the hash marks. At what yard marker does the kicker have maximum angle to the two uprights. Note: You will need to find out the width of the uprights and the width of the hash marks...make a sketchpad model. Is there any merit to some comeentators argument to take a penalty in order to have a "better angle" on the field goal kick?
Before we can answer the question above, we must first understand the dimensions of a football field. Football at the college level is played on a field that looks almost exactly the same as a standard NFL field. The size of the field is the same, as are the goal-post and uprights. So, by doing an internet search, I was able to find the dimensions of a NCAA football field (the appropriate information need for this assignment).
Using the above information we were able to construct a NCAA football field using Geometer's Sketchpad. Also, using the measurements above we were able to graph points on a coordinate grid
by marking vectors and translating the given points above.
Let's look at the following GSP construction:
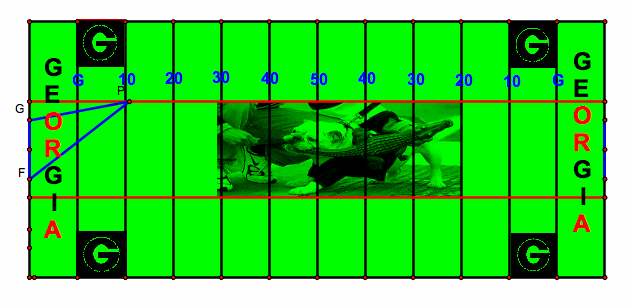
Using Geometer's Sketchpad, angle FPG was measured. As you explore with the attached GSP file you will see that, when kicking from the hash mark, the angle gets worse contrary to some commentators beliefs.
As we investigate the construction above, we ask ourselves at what yard marker does the kicker have maximum angle to the two uprights (assuming the kick is from the hash mark)?
The picture above is drawn to scale of a real NCAA football field. Point G represents the right side of the goal posts and point F represents the left side of the goal posts. Point P represents where the ball is located. If you drag point P, the angle to the uprights will change. After manipulating the points in our construction, we find that the largest angle to the goal posts is actually in the end zone. If we could take away the constraints of the rules of football, then the greatest kicking angle is estimated to be about ![]() when the ball is 6.88 yards away from the goal posts.
when the ball is 6.88 yards away from the goal posts.
However, in college football, field goals are attempted from at least seven yards behind the line of scrimmage. Therefore the realistic angle would be from the seven yard line, which in this case is
![]() .
.
We noticed that as the ball moves further and further away from the goal posts the angle gets smaller and smaller.The higher angle would be when the ball strikes the top of the goal post. So therefore, it doesn't make sense to receive a penalty to get a better angle at the field goal. When teams take a penalty they are pushed back some yards thus decreasing the angle to the goal posts.
If you would like to explore kicking angles with the GSP file to see the "better angle", press the attachment to the right. Field Goal Post (manipulate the location of the ball)