Tangent Circles
By: Erica Fletcher
The purpose of this investigation is to explore tangent circles. First I will discuss the construction of certain types of tangent circles.
First consider a circle within a circle.
Secondly, this investigation begins with the following problem.
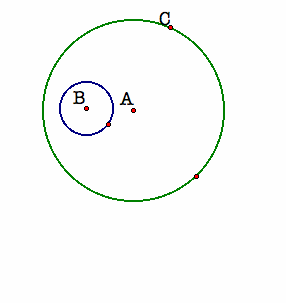
Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.
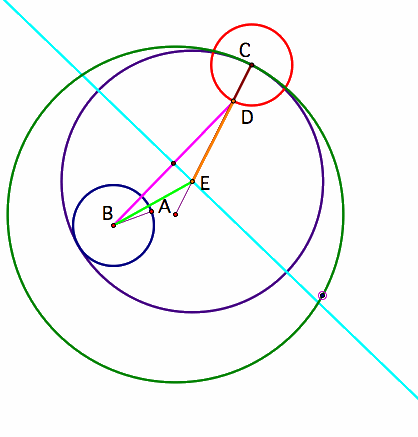
Two circles of non-equal radius are said to be tangent to each other if they meet at only one point. So we will construct a circle that is tangent to 2 other circles. The first thing we will do is draw the two circles. Then we will place an arbitrary point on the green circle and call this point C. Next we will construct a line that passes through both point A which is the center of the green circle and point C. Last but definitely not least after constructing this line we will construct a red circle with the radius of the smaller circle and centered at point C.
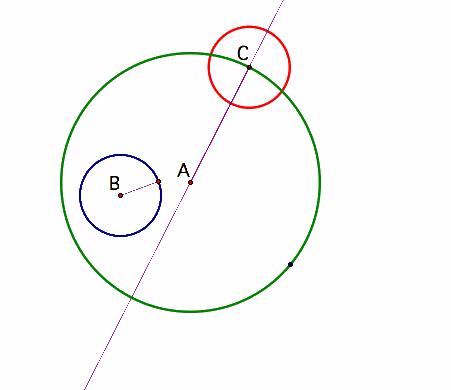
Connect points D and B (below), this will be the base of an isosceles triangle. To construct this isosceles triangle, draw in the perpendicular bisector of segment AC to find point E.
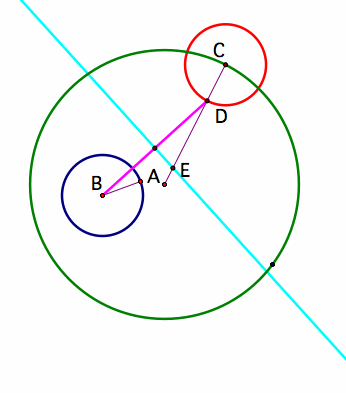
Now using segment CE as a radius, construct the purple tangent circle. This will be tangent to the outside of the blue smaller circle since the radii of these two circles are the same.