

Assignment 9
By: Erica Fletcher
Let triangle ABC be any triangle. Then if P is any arbitrary point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC (lines extended) locate three points D, E, and F that are the intersections. Triangle DEF is the Pedal Triangle for Pedal Point P.
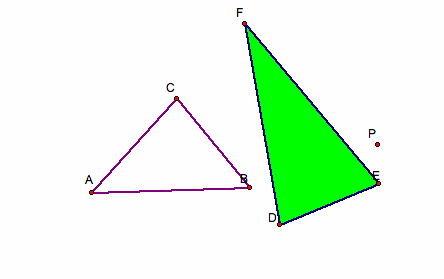
For this investigation we will explore what happens to the pedal triangle if the pedal point is the centroid, incenter, circumcenter, and orthocenter.
First we will start by observing what happens if the pedal point P is the centroid of the triangle ABC.
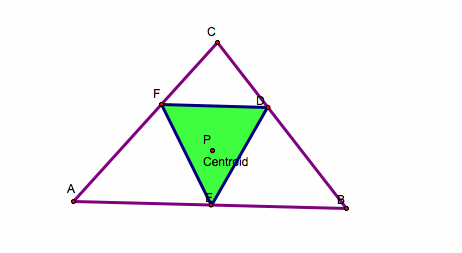
We notice that the pedal point stays inside of the triangle.
Look here if you would like to explore with the GSP construction when the pedal point P is the centroid.
Now let's observe what happens when the pedal point is the incenter of triangle ABC.
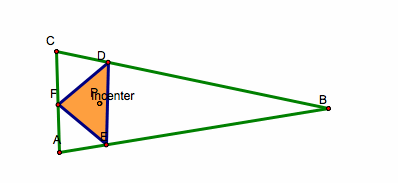
We notice that the pedal point is inside of triangle ABC and DEF no matter where you move it as long as the pedal point P is the incenter. It doesn't matter if we have a right, acute, or an obtuse triangle ABC, the pedal point P will always lie inside of its original triangle.
Look here if you would like to explore with the GSP construction when the pedal point P is the incenter.
Next, we will explore what happens when the pedal point P is concurrent with the circumcenter.
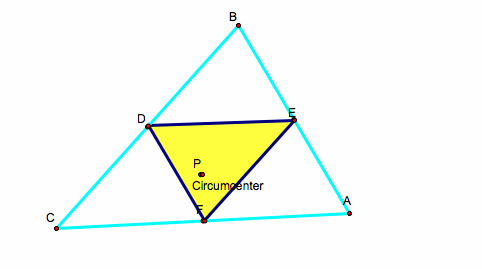
If the original triangle is an acute triangle we see that the pedal triangle stays inside of the original triangle. All of the vertices of the pedal triangle are at the midpoint of the sides of the original triangle ABC. This pedal triangle now looks familiar to one of our script tools we created in Assignment 5. It is the medial triangle! As the pedal point becomes concurrent with the circumcenter, the vertices approach the midpoint of each side of the given triangle because of the fact that the circumcenter is the intersection of the perpendicular bisectors of the sides of triangle ABC.
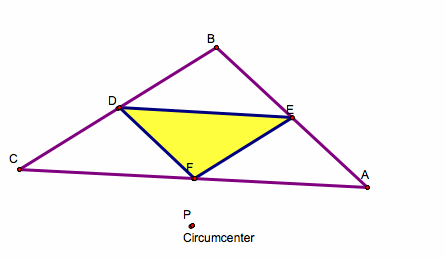
Look above and see that when the original triangle ABC is an obtuse triangle, the pedal P will be on the outside of triangle ABC and DEF.
Look here if you would like to explore with the GSP construction when the pedal point P is the circumcenter.
Lastly, we will examine what happens when the pedal point P is the orthocenter of triangle ABC.
Recall that the orthocenter of a triangle is the intersection point of the three lines that contain the altitudes of triangle ABC.
If we look at the altitudes of the pedal triangle we see something interesting happen.
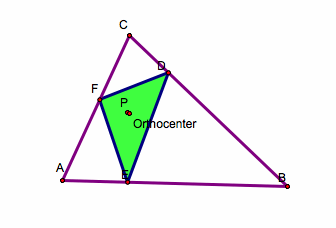
It looks as if the pedal triangle is now the orthic triangle as long as the original triangle is an acute triangle. However, when triangle ABC is obtuse we see that the pedal point will always lie outside of our original triangle.
Click here to see what happens to the pedal triangle when you make triangle ABC an obtuse triangle.
Return to Fletcher's EMAT 6680 Home Page