LUNES
What are Lunes?
A lune is a two-sided figure roughly shaped like a cresecent moon. In fact, the word lune comes from the Latin word "luna", meaning moon. These figures can exist in both plane geometry and spherical geometry.
SPHERICAL GEOMETRY
In spherical geometry, great circles are defined as
those circles of intersection that share the same radius and same center as the
sphere it intersects, and divide a sphere into two equal halves. The great circle is the largest
possible circle able to be formed along a sphere.

(Picture source: http://www.uwosh.edu/faculty_staff/szydliks/elliptic/elliptic.htm)
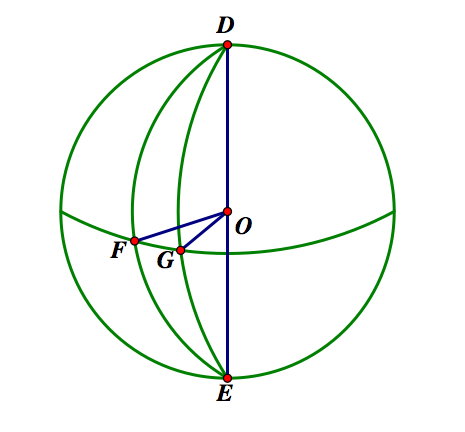
In the image above, the angle of the lune is the angle GOF.
The area of the lune is the same proportion of the area of the sphere as the angle is a proportion of 2pi radians. So, the area of a lune in spherical geometry = ((angle of lune)/2pi)(area of sphere) =
(angle of lune/2pi)(4pi(r^2)) = 2(angle of lune)(r^2), where r is the radius of the sphere.
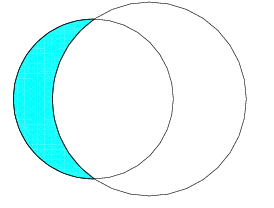
In plane geometry, a lune is the area bounded by two circular arcs. In the image below, the lune is colored light blue.
Greek mathematician Hippocrates proved that lunes are quadrable, or it is possible to construct a square having equal area to that of the lune. While Hippocrates did not show that all such figures are quadrable, he did show that the particular lune he created was.
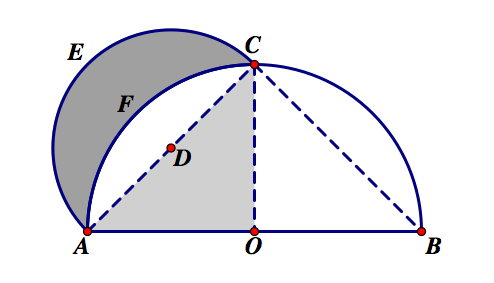

In fact, there are five quadrable lunes. In an attempt to square the circle, Hippocrates squared the lune showed above. He is also credited with finding two other squarable lunes. In 1934, Russian mathematician Tschebatorev came close to finding a solution, which his student Dorodnov completed in 1947, ending the search for other quadrable lunes.
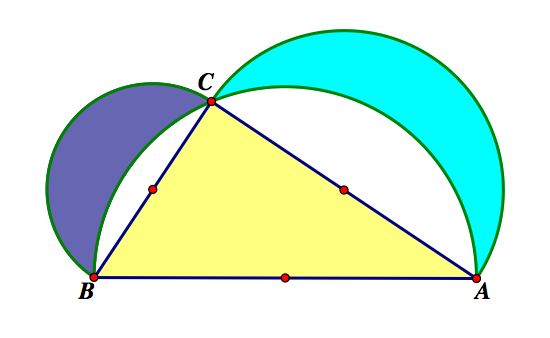
Hippocrates also showed using a proof similar to the one above that if two lunes are formed on the sides of a right triangle (their inner boundary being the circumcircle of the triangle and their outer boundaries being circles with diameters equal to the side lengths), then the sum of the areas of the two lunes is equal to the area of the triangle. In the figure shown below, the sum of the areas of lunes BC and AC are equalivalent to the area of the triangle ABC.