Spherical Geometry
Spherical Geometry in History
At the time when Earth was
discovered to be round rather than flat, spherical geometry began to emerge to
aid navigators in mapping the land and water. However, even before
Columbus, ancient Greek and Phoenician mariners used the ideas of spherical
geometry in naval explorations of the world they knew. Contrary to popular belief, it was
indeed Ptolemy, not Christopher Columbus, who discovered that the Earth was
spherical.
Ptolemy, the man shown to the left, said, “If the earth were
flat from east to west, the stars would rise as soon for westerners as for
orientals, which is false. Also, if the earth were flat from north to
south and vice versa, the stars, which were always visible to anyone, would
continue to be so wherever he went, which is false. But it seems flat to
human sight because it is so extensive.”
As much as 2000 years ago, the discovery of the Earth’s curved surface
was making huge impacts on the way the Earth was viewed and mapped.
The basic element of
spherical geometry is the sphere, a three-dimensional surface made up of the
set of all points in space at a given distance from a fixed point called the
center. If we take an arbitrary plane and sphere lying in the plane, there are
three possibilities for their intersections. First, the plane and the sphere
never intersect. Secondly, the
plane may lay tangent to the sphere forming one distinct point of
intersection. In the final
case where the plane passes through the sphere, the in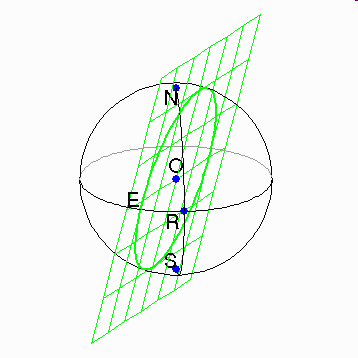
tersection
forms a circle. Within this final case there lies a unique
case. If the plane passes through
the center of the sphere, the circle formed is known as a great circle. In the diagram to the right, Point O represents the sphere’s
center, and the great circle is represented by circle E. The
Great circles are defined as
those circles of intersection that share the same radius and same center as the
sphere it intersects, and divide a sphere into two equal halves. The great circle is the largest
possible circle able to be formed along a sphere, such as the Earth’s equator. Interestingly, all of Earth’s lines of
longitude are great circles, yet the Equator is the only line of latitude that
is a great circle.
Spherical geometry is defined
as the study of figures on the surface of a sphere, and it can be viewed as the
three-dimensional version of Euclidean or planar geometry. Although closely related, the two ideas
of spherical and planar geometry are completely different. Most students who
have taken a high school level geometry course can recite some of the basic
facts of planar geometry: two parallel lines never intersect, the sum of the
interior angles of a triangle is equal to one-hundred and eighty degrees, and
the shortest distance from one point to the next is a straight line. Yet, these concepts do not hold in
spherical geometry.
Properties of Spherical Geometry
In spherical geometry, there
are no parallel lines. In fact,
there are no straight lines.
Therefore, in spherical geometry, a great circle is comparable to a line. There are no straight lines in
spherical geometry. Instead, the shortest distance from one point to the next lying on a
sphere is along the arc of a great circle. On a sphere, the angle between two curved arcs is measured
by the angle formed from the intersection of the lines lying tangent to the two
arcs.
When three curved arcs intersect one
another, a spherical triangle is formed. A spherical triangle is any
three-sided region enclosed by sides that are the arcs of great circles. Spherical
triangles can have angle sums that range between one hundred eighty degrees and
five hundred forty degrees. Spherical triangles can have angle sums larger than
the usual one hundred eighty degrees found in a triangle because lines
connecting points have a slight curve to them. Even so, spherical triangles can
have ninety-degree angles just like triangles in the plane.
Differing from Euclidean
geometry, two spherical triangles are not only similar, but congruent if they
share the same angles. If one of
the angles of a spherical triangle is a right angle, the triangle is known as a
spherical right triangle, and a Spherical Pythagorean Theorem exists. In a
spherical right triangle, let C denote the length of the side opposite the
right angle.
To
calculate the area of a spherical triangle on a unit sphere, one must sum the
angles of the spherical triangle (in radians) and subtract pi. For example, say
a spherical triangle had two right angles and one forty-five degree angle. To
find the area of the spherical triangle, restate the angles given in degrees to
angles in radians. Thus, we are working with a spherical triangle with two pi/2
angles and one pi/4 angle. Add the three angles together (pi/2 + pi/2 + pi/4). Thus, the angles total 5pi/4. Subtract
pi from 5pi/4 to find the area of the spherical triangle. Therefore, we have a
total area of pi/4 units squared.
It has been established that
a great circle is formed from a plane that intersects a sphere through its
center. In analyzing two great
circles that lie in a sphere, the two planes that form the great circles must
intersect in a line, which in turn intersects the sphere at two distinct
points. Therefore, two great
circles intersect each other at two antipodal points. The planes also divide the sphere into four parts. These regions are known as lunes, which
comes from the Latin word “luna,” meaning moon. A lune is a two-sided polygon lying on a sphere. 
To find the area of a lune,
one must know the lunar angle and the formula 2R2(lunar angle),
where R represents the radius of the sphere. If the lunar angle is not given,
find p(pi)/q, where p represents the
union of the lunes and q is the number of equal lunes drawn in a hemisphere.
Knowledge about a lune’s area can be helpful in solving the area of the sphere.
For example, say the area of a lune is thirty-two centimeters squared, and we
want to find the area of the sphere where the lune is present. The area of
a sphere is 4piR2, where R represents the radius. Since we know the
formula for the area of a lune, we can solve for the radius, the unknown
variable. Then we can use the radius in the formula for the area of the sphere
to solve for the area of the sphere. After a few calculations, we can see that
the radius is four centimeters. We then can square this and multiply the new
result by 4pi. Thus, we have the sphere’s area equal to 64pi centimeters
squared.
In two dimensions, a lune is a plane figure bounded by two circular arcs. Greek mathematician Hippocrates proves that lunes are quadrable, or it is possible to construct a square having equal area to that of the lune. While Hippocrates did not show that all such figures are quadrable, he did show that the particular lune he created was.
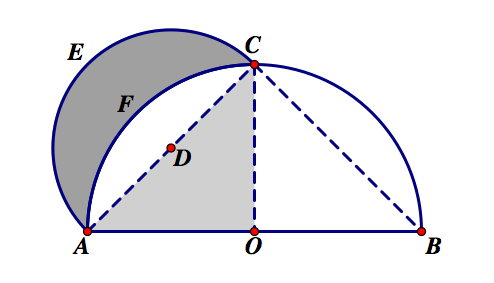
In fact, there are five quadrable lunes. In an attempt to square the circle, Hippocrates squared the lune showed above. He is also credited with finding two other squarable lunes. In 1934, Russian mathematician Tschebatorev came close to finding a solution, which his student Dorodnov completed in 1947, ending the search for other quadrable lunes.
As discussed earlier, the
shortest distance between two points on a sphere is along the arc of a great
circle. In spherical geometry,
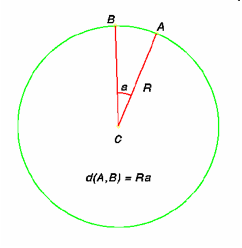
there exists a formula to find this distance. Given two points A and B, first locate the angle (measured
in radians) that is created between the two pointsand the center of the
sphere. Then, multiply by the
radius (R) of the sphere, giving the formula d(A,B)= Ra, where a represents the
angle formed between points A and B. For example, to find the distance between two
points A and B with an angle of pi/4 between them on a sphere having a radius
of 4, we multiply pi/4 by the radius length of 4 units to get a spherical
distance of pi.
Where can I find Spherical Geometry today?
Today, the concepts of
spherical geometry are implemented in air and space travel, naval cruises, and
much more. For example, an
airplane looking to travel from Florida to the Philippines would pass over
Alaska. Since the Philippines lie
south of Florida, it does not seem reasonable to take this flight route. Yet, this happens to be the shortest
distance between the two points, since Florida, Alaska, and the Philippines lie
relatively “collinearly” along the path of a great circle. Thus, the best path
to travel from Florida to the Philippines would include a flight route over
Alaska.
Ptolemy: http://www.staff.science.uu.nl/~gent0113/eclipse/astro/almagestephemeris.htm
Intersection of Sphere and Plane: http://math.rice.edu/~pcmi/sphere/sphere.html
Lune: http://www.uwosh.edu/faculty_staff/szydliks/elliptic/elliptic.htm
Spherical Distance: http://math.rice.edu/~pcmi/sphere/gos2.html