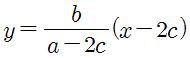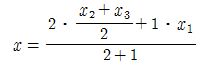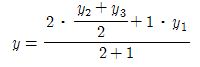Medians of a triangle
by Hwa Young Lee
What is the centroid of a triangle? A centroid (center of mass) of a triangle is the intersection point of the three medians of the triangle. A median of a triangle is the segment joining a vertex to the midpoint of the opposite side.
Here, we are going to explore several properties of the centroid of a triangle.
1. Do the three medians of a triangle always intersect at one point?
The existence of a centriod: The three medians of a triangle are concurrent.
First, we are going to use the coordinate plane to show that the medians of a triangle are concurrent and thus any triangle has a centroid.
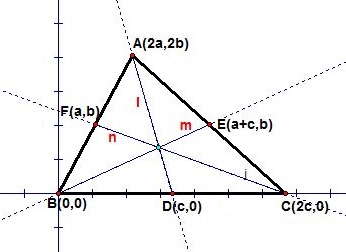
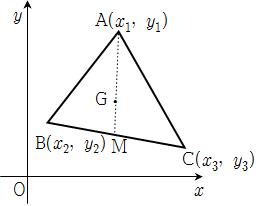
Let's name our triangle ABC and for simplicity, carefully place vertex B on the origin and the side BC of the triangle on the x-axis. Then again, for notational convenience, let's label our vertex A's coordinates as (2a, 2b) and C's coordinates as (2c, 0). In this case, since we formed a triangle, a , b and c are all not equal to zero. Next, we need to find our medians. Since the medians are the segments from a vertex to the midpoint of the opposite side, let's label the line extensions of medians from A, B, C to their opposite midpoints D, E, F as l, m, n, respectively. This is what we want:
Since our goal is to show that the three medians are concurrent, we are first going to find the intersection of two of the medians l and n by viewing them as lines (which is obvious that they meet, since their slopes are not parallel). After that, all we need to do is show that the third median (line m) passes through that intersection point!
Okay, so first let's find the equations of line l and line n.
Line l passes two points (2a, 2b) and (c, 0), and line n passes two points (a, b) and (2c, 0). Using these points we can find the equations of the two lines.
l:
and n:
Then
,
and
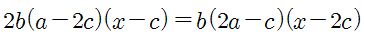
so
.
Solving this for x,
.
Plugging this x-value in any of the equations for line l or n, we obtain the y-value of the intersection:
.
Thus, the intersection is
.
Meanwhile, line m passes the origin and point (a+c, b), so the equation of line m is
m:
.
Now we show that
, as required.
This also shows that when finding the centroid of a triangle, we only need to find the intersection of two of the medians (because the third would meet at that point anyway!).
2. Now that we know we can always find the centroid of a given triangle, we show that the centroid is
the distance from a vertex to the midpoint of the opposite side.
The centroid is
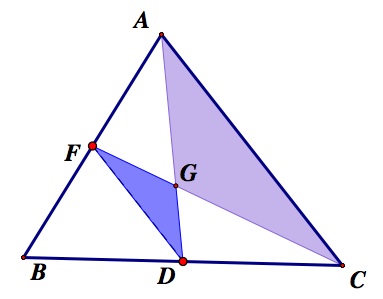
First, let's name our centroid G and connect points D (the midpoint of AB) and F (the midpoint of BC).
As in the figure above, since D and F are midpoints of segment BC and AB respectively, AC//FD and AC=2FD.
Thus, triangle GFD and triangle GCA are similar (AA) with a ratio of 1:2. Hence, CG:GF=AG:GD=2:1.
Similarly, connecting E (the midpoint of AC) and F (the midpoint of AB), we can easily see that BG:GE=2:1.
Thus, the centroid of a given triangle is
Using this fact, we can actually find the coordinates of a centroid when given the coordinates of the three vertices of the triangle.
Let. We have the following figure:
Since M is the midpoint of BC,
.
From our second investigation, we found out that G divides segment AM by 2:1.
Thus,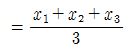
and
.
Hence the coordinates of the wanted centroid is
.
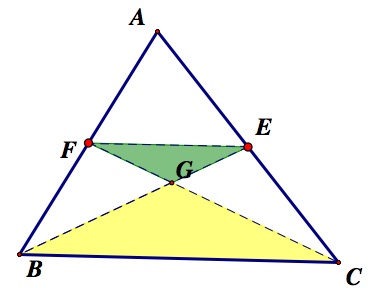
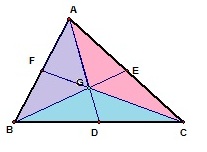
3. Now, let's divide a triangle by the three medians into six small triangles.
The three medians of a triangle divide the triangle into six small triangles. These triangles all have the same area.
Let's take a look at our cut up triangle and color the small triangles that we know have the same area in the same color.
Since we know that D, E, F are midpoints of each sides of the triangle, we can see that triangles GAB, GBC, GCA are all equally cut in half area-wise by GF, GD, GE, respectively. So, we can see that the following triangles colored in the same color have the same area.
Meanwhile, AF=BF, BD=CD, and CE=AE. Thus, ABD=ACD and ABE=BCE.
For convenience, let's say the area of one purple triangle is p, the area of one blue triangle is q, and the area of one pink triangle is r.
Then since ABD=ACD, 2p+r=2q+r, so p=q and since ABE=BCE, 2p+q=2r+q, so p=r.
Hence, p=q=r and this shows us that the six small triangles are of the same area!
