Pedal Triangles

by Hwa Young Lee

In assignment 4 and assignment 6, we explored the medians of a triangle, the centroid, and the triangle constructed by the medians of a given triangle.

In assignment 8, we explored the orthocenter of a triangle and the ratio of line segments on the lines containing the altitudes, divided by the orthocenter.

Here, we are going to explore pedal triangles when the pedal point is on one of the centers of a given triangle.

What is a pedal triangle and a pedal point?

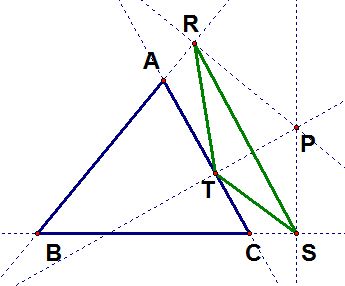
For a given triangle ABC, we can construct perpendiculars from a given point P on the plane to the three sides AB, BC, and CA (extended if necessary). If we name the intersection points R, S, and T respectively, then we can form a triangle RST. This triangle RST is the pedal triangle for pedal point P of triangle ABC.

We can find many pedal triangles of a given triangle by moving the pedal point around on the plane.

Simply, we can think of two cases, when the pedal point is outside the triangle:

or when the pedal point is inside the triangle:

Now what happens if the pedal point is one of the centers of the triangle? More specifically, what if the pedal point P is the 1) centroid, 2) incenter, 3) orthocenter or 4) circumcenter of triangle ABC?

1)

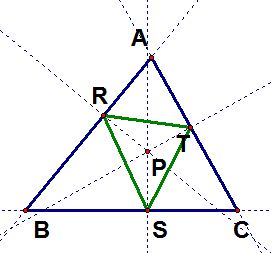
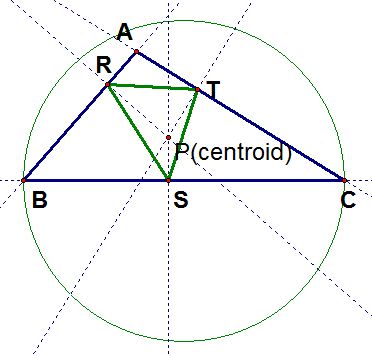
When the pedal point P is the centroid of triangle ABC, move around the vertices of the triangle and explore in a GSP construction. Can you find any interesting conjectures?

A centroid of a triangle is the intersection point of the three medians of the triangle. A median of a triangle is the segment joining a vertex to the midpoint of the opposite side.

From our figure on the left, it is hard to find any specific conjectures of the pedal point P and the pedal triangle RST.

Let's explore different triangles ABC in order to see if we can find anything interesting.

 

 

a) triangle ABC is acute
b) triangle ABC is a right triangle
c) triangle ABC is obtuse

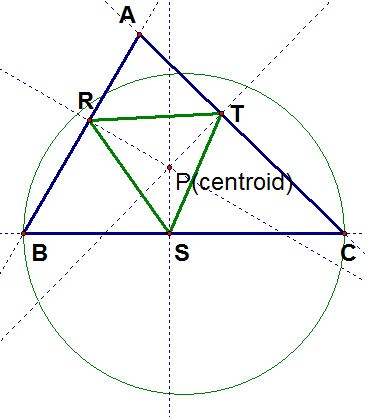
Note that to make sure triangle ABC is acute, right, or obtuse, we can use the fact that when BC is the diameter of a circle then A is a right angle. By merging point A to the circle, we know that we have constructed a right triangle ABC. When A is outside of the circle, we have an acute triangle and when A is inside the circle, we have an obtuse triangle.

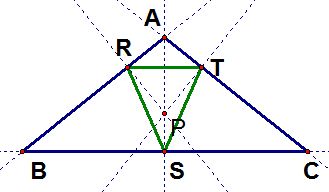
In these three cases, it is difficult to find any specific properties of the pedal point or the pedal triangle due to the fact that it is at the centroid.

So, let's try other triangles.

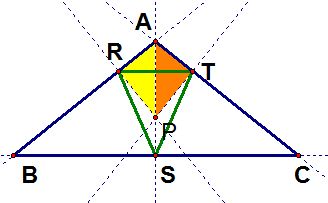
d) triangle ABC is an isosceles, with AB=AC e) triangle ABC is an equilateral

d) Well, if the triangle is isosceles, the pedal triangle looks isosceles, too.

So we conjecture when is an isosceles, with , then the pedal triangle RST is an isosceles as well.
Proof:

First, we show that triangles APR and APT are congruent.
Since , the median from vertex A is the perpendicular bisector of side BC and thus the pedal point P(which is the centroid) is on . bisects angle A. Hence, .

Also, by the definition of the pedal triangle, , which leads us to .

is the common side. Thus (ASA).

This implies that and thus .

Also, we know that . Since is an isosceles, and thus (SAS).

Therefore and thus the pedal triangle RST is isosceles with .

 

 

 

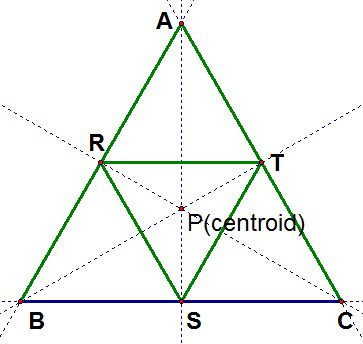
e) If the triangle is equilateral, it seems like the pedal triangle should be equilateral.

So we conjecture when is equilateral, then the pedal triangle is equilateral as well.

It is pretty obvious from the experience with the isosceles, so here we use a short proof.

Proof:

When is equilateral, then the medians are the perpendicular bisectors of each side.

Thus, we know that R, S, and T are the midpoints of each side.

This implies that

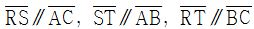
and (by the midpoint theorem).

Hence  , which shows us that the pedal triangle is equilateral!

 

 

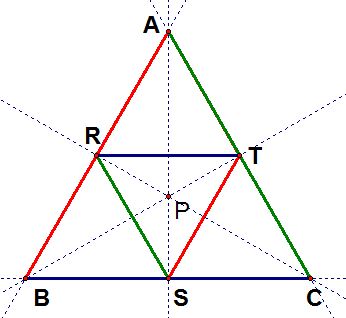
2)

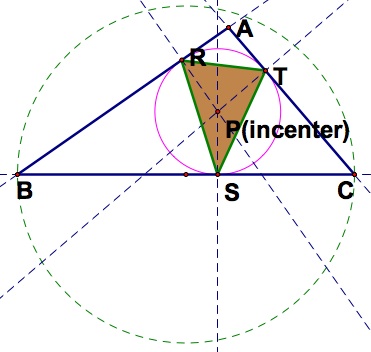
When the pedal point P is the incenter of triangle ABC, move around the vertices of the triangle and explore in a GSP construction. Can you find any interesting conjectures?

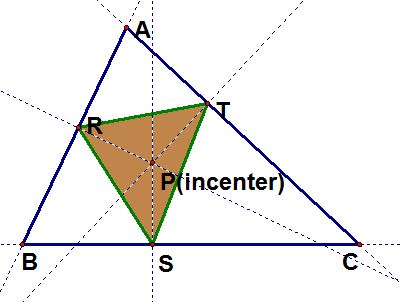
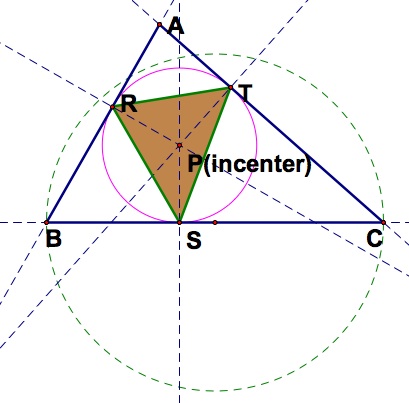
The incenter of a triangle is the point in the interior of the triangle that is equidistant from the three sides. We can find the incenter by finding the intersection of bisectors of each angle of the triangle.

Thus, for any triangle ABC, the pedal triangle is the inscribed triangle of the inscribed circle. In other words, the pedal point P becomes the circumcenter of the pedal triangle RST.

 

a) triangle ABC is acute b) triangle ABC is a right triangle c) triangle ABC is obtuse

More specifically, we investigate two cases:
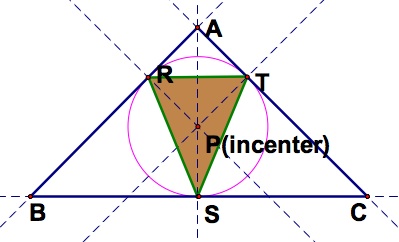
d) triangle ABC is an isosceles, with AB=AC
e) triangle ABC is an equilateral

d) If the triangle is isosceles, the pedal triangle looks isosceles, too.

So we conjecture when is an isosceles, with , then the pedal triangle RST is an isosceles as well.

Proof: Since , the angle bisector of angle A is the perpendicular bisector of side BC. Thus, the proof follows the proof for the centroid when is isosceles and shows us that the pedal triangle is also isosceles.

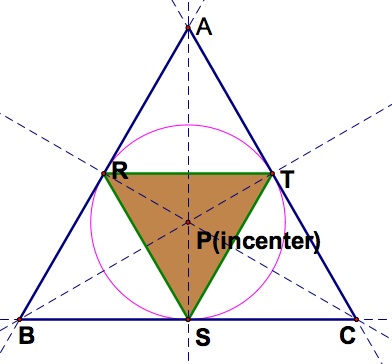
e) If the triangle is equilateral, it seems like the pedal triangle should be equilateral.

So we conjecture when is equilateral, then the pedal triangle is equilateral as well.

It is pretty obvious from the experience with the isosceles, so here we use a short proof.


Proof: When is equilateral, then the angle bisectors of each side become the perpendicular bisectors of each side.

Thus the proof follows the proof for the centroid when ABC is equilateral and shows us that the pedal triangle is equilateral!

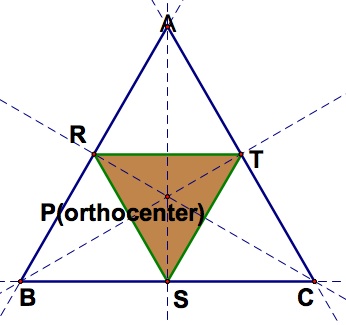
3)

When the pedal point P is the orthocenter of triangle ABC, move around the vertices of the triangle and explore in a GSP construction. Can you find any interesting conjectures?

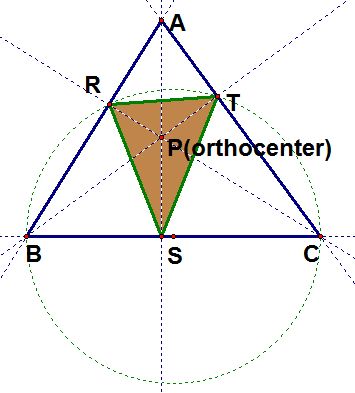
The orthocenter of a triangle, is the intersection point of the three lines containing the altitudes of the triangle. An altitude of a triangle is the perpendicular segment joining the vertex to the opposite side.

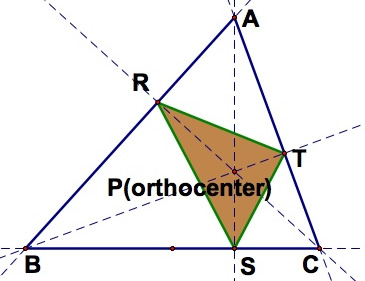
When the pedal point P is the orthocenter, the pedal triangle is formed by the feet of the lines containing the altitudes, which is called the "orthic triangle". Thus, the position of the pedal triangle will depend on whether the triangle is acute, right, or obtuse (In assignment 8, you can see how the orthocenter is differently positioned in each case).

a) When is acute, the orthocenter is in the interior of the triangle and thus the triangle formed by the feet of the altitudes form the pedal triangle, which is inside .
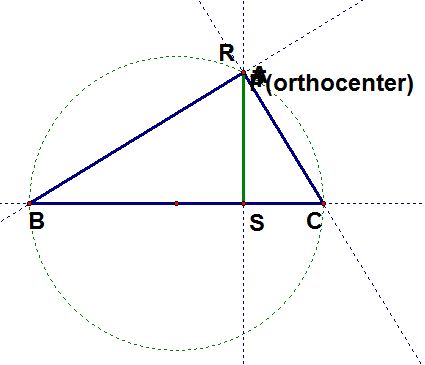
b) When is right, the orthocenter is on the vertex with the right angle (A in this case). Thus, the pedal triangle does not exist.
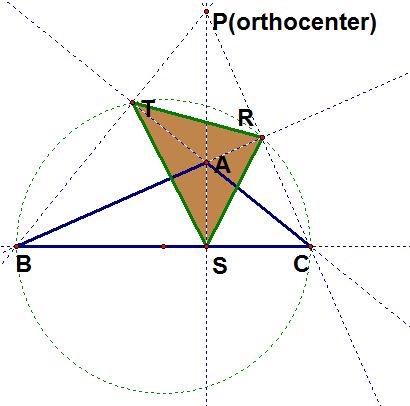
c) When is obtuse, the orthocenter is outside the triangle and the pedal triangle is either outside or inside . The two triangles partially overlap. Also notice the two vertices of the pedal triangle that are outside of are both on the circle with BC the diameter. (This is due to the definition of the pedal triangle. Can you see why?)

a) triangle ABC is acute b) triangle ABC is a right triangle c) triangle ABC is obtuse

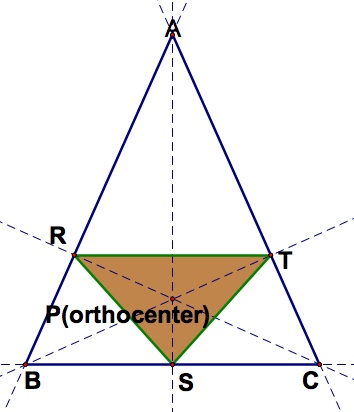
Can you make any conjectures about the pedal triangle when is isosceles or equilateral?
d) triangle ABC is an isosceles, with AB=AC e) triangle ABC is an equilateral

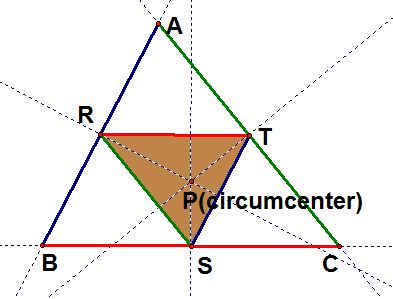
4)

When the pedal point P is the circumcenter of triangle ABC, move around the vertices of the triangle and explore in a GSP construction.

The circumcenter of a triangle is the point in the plane that is equidistant from the three vertices.

We can find the circumcenter by finding the intersection of perpendicular bisectors of each side of the triangle.

Thus, for any triangle ABC, the pedal triangle is the medial triangle which connects the midpoints of each side of the given triangle.

From this, we know from the midpoint theorem that
and

.
Moreover, with a ratio of 2:1 (SSS).