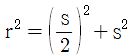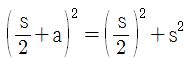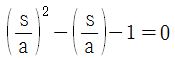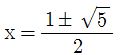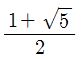Square inscribed in a semicircle
by Hwa Young Lee
Final assignment 2. Square Inscribed in a Semicircle: Find a Ratio
This is a GSP construction of this figure.
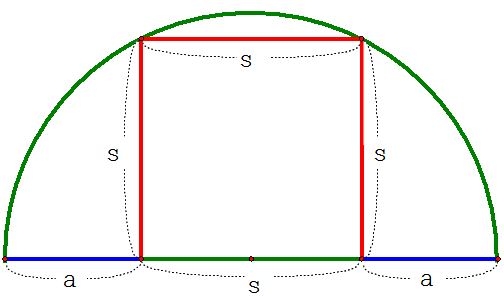
Given a semicircle with an inscribed square of side s, let a be the length on the diameter on each side of the square.
Let's find the ratio of the length of the side of the square to the length on the diameter on each side of the square.
In other words, let's find
.
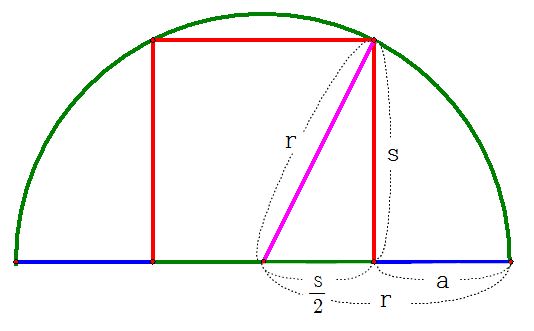
We want to use the fact that we have a semicircle and square. If we add a magic line, it is pretty easy to find the ratio:
First of all, we know that the midpoint of the bottom side of the square is the center of the semicircle.
Hence, if we let the radius of the semicircle r, then we know that
Also, we have a right triangle formed by the magic line and the side of the square and half the side of the square.We use the Pythagorean Theorem and have
Plugging in
, we have
With a little expanding and canceling out, we are left with
Dividing out by(a is nonzero),
Substituting
as x, all we need to do is solve
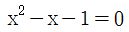
and find the value of our ratio!
Using the quadratic formula, we get
but since a and s are both positive (lengths), our wanted ratio is
the golden ratio!
We earlier found the golden ratio in the Fibonacci sequence using the spreadsheet in assignment 12.