ANCIENT EGYPTIAN MATHEMATICS AND COMPUTERS

By Leighton McIntyre

Mathematical Documentation of the Ancient Egyptians

Early Egyptians carved their numbers (hieroglyphic writing) in temples , vases, and stone monuments. Later they developed writing on papyrus (plural papyri). Papyri were easily destroyed but two important papyri still exist to date. They are the Rhind (Ahmes ) Papyrus for which the name of the scribe was Ahmes in 1650 BC and the Moscow Papyrus for which no scribe was named. Both the Rhind(Ahmes ) papyrus and the Moscow papyrus contain problems that involve practical applications as well as the manipulation of number system without any given practical applications. Many of the problems involved division and multiplication even involving fractions. For example the first six problems of the Rhind(Ahmes ) papyrus asks how to divide n loaves of bread between 10 men. The Rhind(Ahmes ) papyrus contains 87 mathematical problems while the Moscow papyrus contains 25 mathematical examples.

Rhind (Ahmes) Papyrus.

Moscow Papyrus.

The Ancient Egyptian Number System

The Egyptian Number system uses one stroke (I) to represent the number a symbol looking our symbol for set intersection (Ç) to represent 10, a picture looking like a coiled rope to represent 100, . For 1000 the symbol was a water lilly with the leaf stem and rhizome of the root showing. For 10,000 the symbol was a very large finger. The symbol for 1000000 was a frog in full spawn. For 1000000 the symbol was that of the God Heh with outstretched arms and kneeling on one knee. The symbol for infinity was similar to what we use today . It looked like a full circle with bows on the ends. Egyptian numbers were called hieroglyphics and the following display shows what their symbols represent in our decimal system.

Source: www.math.wichita.edu

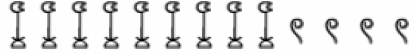
Representing the numbers one through nine involved writing down 1 through 9 strokes side by side. An so representing very large numbers became cumbersome. So 99 was written like this .Look at nine thousand nine hundred and ninety nine. . So you see that the numeral representations can take up quite a bit of space pretty quickly.

Ancient Egyptian Calculations

So how did the Egyptians use these symbols in their calculations? Lets start with addition. Lets say they were adding one plus one well that was easy. One strike plus one stroke gives a double stroke that is I plus I = II. Then representing I00 minus 1 we have minus I =

For multiplication the Egyptians used a system of doubling and halving . They were really using a binary system in this case where the numbers 0 and 1 were only two levels for the place holders To multiply any 2 numbers for example 32 times 15, you divide the first number by two until the answers reaches 1 and them multiply the other number by 2 the same number of times that you divided the first number by 2.

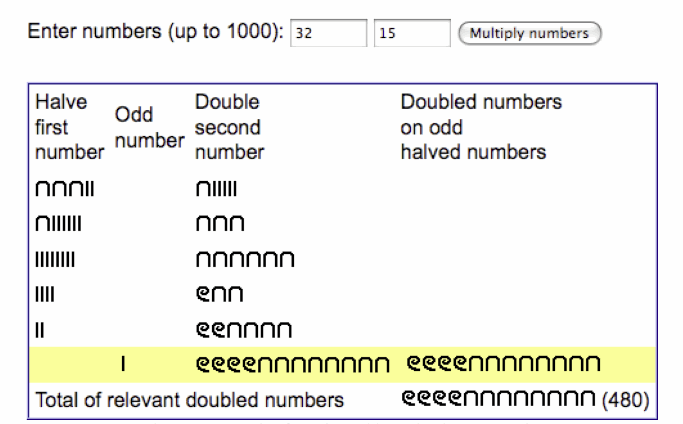
Diagram generated using an applet from http://gwydir.demon.co.uk

If it is not possible to divide the numbers evenly until it goes to one then you subtract one before halving the first number.

Diagram generated using an applet from http://gwydir.demon.co.uk

Since the Egyptians did not base a base 10 system for multiplication their system which was a binary system would seem rather cumbersome to us today. However it works. It is easy because you only had to work with two levels 0 and 1. So check this 0x0=0, 0x1=0,1x0=0,1x1=1, yes so easy. Thus you don’t have to add any numbers on the zero lines because zero times any number is zero and given that 1 times any number remain the same number than all that has to be done is just to add the numbers to get the final answer.

Egyptian Mathematics and Computers

Believe it or not, modern day computers do not use a cumbersome ten digit decimal system to process information. Instead a computer processes information in zeros and ones; exactly the same way that the same way that Ancient Egyptians manipulated their number system. An information system needs at least two characters to function and the binary system is the smallest one that can be used. Even tough the binary system used more characters as place holders

Computers are a form of digital electronics and digital electronics function in two states ‘on’ or off’. The levels of voltage in an electronic device can be the indicator of ‘on’ of ‘off’. For example a transistor with no voltage is considered off while a transistor with five volts is considered ‘on’. Some computer hardware such as CDs use dark spots on the surface to indicate off and light spots on the surface to indicate ‘on’. Computer hard disks are driven by magnetism but again there are only two states that they operate in that is ‘on’ and ‘off’. The computer memory also has two states ‘on’ and ‘off’ which are achieved by changing electric charges in the capacitors. Because the computer devices essentially have two states then it is pretty easy for numbers to be encoded in the computer in a binary number system rater than a decimal number system. Take for example a number like 18 in decimal number system is equivalent to the number 10010. In computer language this is simply ‘on’, ‘off’, ‘off’, ‘on’, ‘off’. In this way all numbers can be manipulated in the two different states of the computer when 1 is treated as ‘on’ and 0 is treated as ‘off’.

Thus although the binary number system will contain more digits than the decimal number system for the same number, the computer can easily used a pattern similar to the ancient Egyptians to add, multiply, subtract, and divide numbers very quickly. Also given that Ancient Egyptians knew that all numbers can be expressed as a power of two and modern computer programmers also know and use the same idea than we can say that there is a logical link between what the ancients Egyptians already knew and what we use today in our computers today. Ancient Egyptians never had to memorize a times table and neither does a computer. Multiplication and division of any number is achieved in both situations by manipulating all numbers as if using a binary number system.

Take for example a calculation like 18 * 32 in the modern day computer is

Power of 2	18 (in binary)	32 doubling	Multiply cool 2 by cool 3 then add
1	0	32	0
2	1	64	64
4	0	128	0
8	0	256	0
16	1	512	512
	= 10010		Total = 576

Thus the computer multiplication is done like the multiplication in ancient Egyptian Mathematics. In the above 1 indicates ‘on’ or ‘electricity’ present, while 0 indicates ‘off’ or no ‘electricity’ present.

Division is done in the reverse order 576 ¸ 32 in computer mathematics is like the following.

576 and powers of 2	32 doubling	Matching levels
1	32	0
2	64	1
4	128	0
8	256	0
16	512	1

In the above table the 32 is doubled until the highest doubling less than 576 is reached. Indicate the level of the power of two that corresponds to this number (512) by a 1. Subtract this number 512 from 576. Note that the remainder is 64. Notice where 64 line up with the powers of 2 column and indicate this by 1. Indicate by 0 the other powers of two levels. Then the binary code for the answer is 10010, which is equal to 18 in the decimal system.

Now using such a system the, calculations can be done quite easily, pretty accurately and efficiently by the computer. This is just like the Ancient Egyptians did it without the use of memorizing times tables.

References