

Proof involving G, H, and C
By Leighton McIntyre
Goal: This write up represents a continuation of the assignment 4 discussion involving the orthocenter (H), the circumcenter (C), and the centroid (G). In this write up I intend to prove that G, H, and C are collinear. I also intend to prove that the length of HG is twice the length of GC.
Proof that G, H, and C are collinear
First I will make GSP sketches of the triangle centers H, G, and C. These are shown below on the same diagram. The orthocenter (H) of a triangle is the intersection of the three altitudes of the triangle. The centroid (G) of a triangle is the intersection of the three medians of the triangle. The circumcenter (C) is the intersection of the three perpendicular bisectors of the triangle.
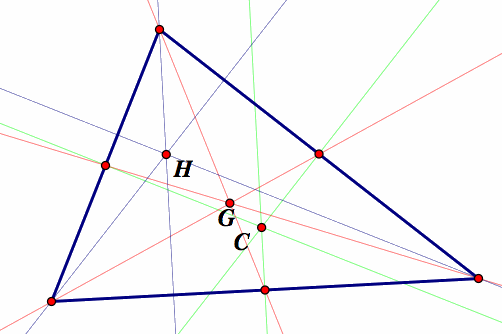
The first proof that HGC are collinear, must show that the three centers lie on a straight line. We can choose any of the two points, draw a straight line through them and then proceed to show that the third point must also lie on this line. For the purposes of this demonstration we choose the points H and G first. We construct a line through HG.
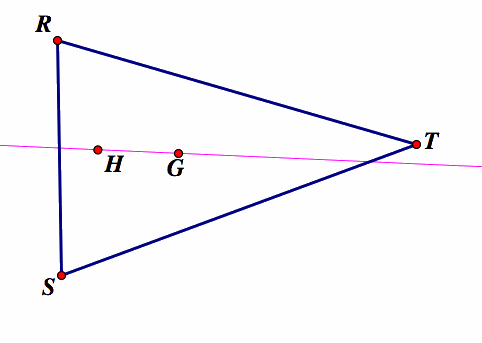
Next we construct one perpendicular bisector to one side of the triangle and mark where this perpendicular bisector crosses the line HG. We will call this point X. We then proceed to show that the other two perpendicular bisectors should also pass through the point X.
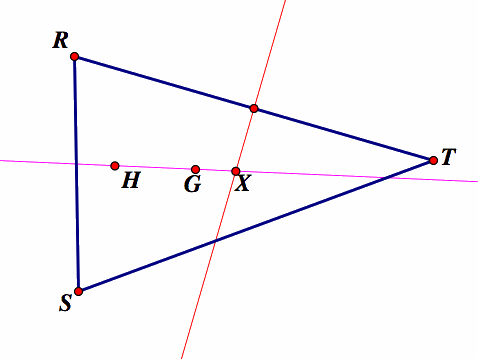
We construct the first perpendicular bisector and labeled the point where it crosses the line GC as X. We then construct the second perpendicular bisector line. After the construction the second perpendicular bisector also passes through the point X.
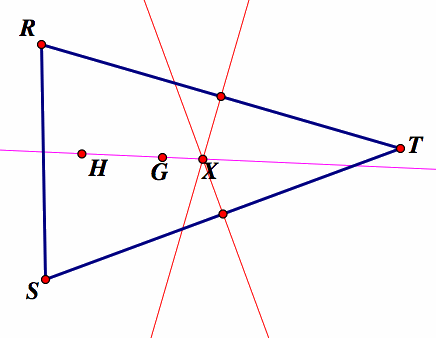
The fact that two perpendicular bisectors constructed in GSP pass through the point X is sufficient to state that the point x will also have the third perpepndicilar bisector passing through it. We proceed to construct one more perpendicular bisector line. If this line passes through X, we can agree that all three perpendicular bisector lines pass though X, and therefore X is the same point as the circumcenter C.
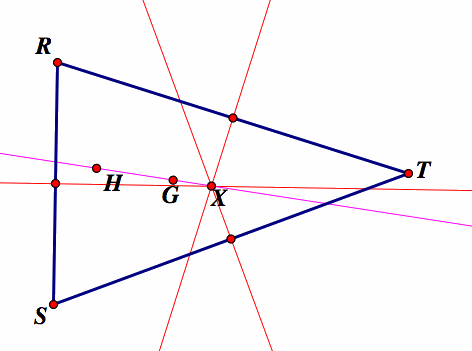
As the diagram above shows, the third perpendicular bisector line also passes through the point X and thus the point X is the same as the circumcenter C.
We conclude that since HGX lie on a straight line and because X is the same as point C, then HG and C all lie on a straight line.
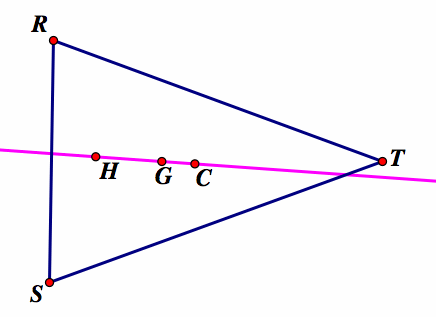
Proof that the length of HG is twice the length of GC (HG = 2GC)
In order to carry out this proof we must note the the centroid G, is 2/3 of the distance from the vertex to the midpoint of the opposite side. We then proceed to use the concept of similar triangles to show that HG = 2GC.
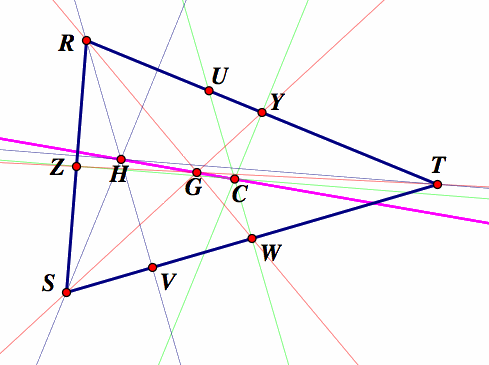
We have shown in the above diagram, the triangle RST with centers H,G and C, along with the line connecting H, G, and C. The midpoints W,Y, and Z, of the sides of the triangle are marked, as well as the altitude foot V and the point U where the perpendicular bisector of one side (ST) of the triangle cuts another side (RT) of the triangle.
Because this diagram is a bit cluttered, we will highlight some sections for our proof.
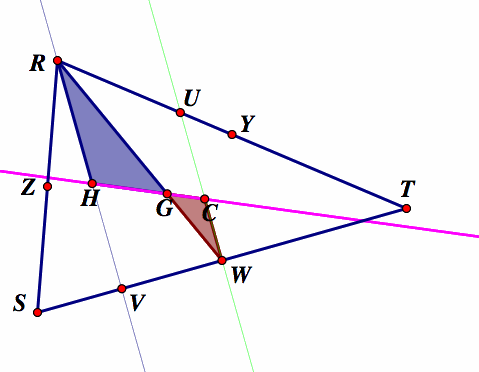
Notice here that the centroid G lies along the median RW, and because a centroid trisects a median, we can see that RG = 2GW.
Lines RV and UW are both perpendicular to line segment ST.
Thus lines RV and UW are parallel to each other.
Angle HRG and angle CWG are congruent by alternate interior angles theorem ( two parallel are lines cut by a transversal producing these angles )
Angle RGH and angle WGC are congruent by vertical angles theorem
At this point we can say that since two pairs of angles in the two triangles GHR and GCW are congruent, then triangles GHR and GCW are congruent by AA Similarity Postulate.
In addition to that, since two pairs of angles in the two triangles GHR and GCW are congruent, we can deduce that the third pair of angles are congruent, because the angles in a triangle sum to 180 degrees (Triangle Angle Sum Theorem). Thus angle GHR and angle GCW are congruent (by the Third Angle Theorem).
Since we know that RG = 2GW, and side RG is similar to side GW.
We also know that side HG is similar to side GC, and thus side HG = 2GC.