

CYCLOID INVESTIGATION
By Leighton McIntyre
Goal : To write parametric equation for a cycloid and demonstrate the path traced by a cycloid.
The Parametric Equation of Cycloid
A cycloid is the curve traced by a point on the circumference of a circle as it rolls on a straight line.
The parametric equation for a cycloid is as follows:
x = a (t - sin t)
y = a ( 1 - cos t)
The line chosen for the rolling is a horizontal line or the x-axis. The parameter t is the variable angle through which the circle rolls while a is the radius of the circle.
Let the initial position of the point on the circle that we choose to focus on be P(0,0), and this point moves through a rotation to P(x,y)
The radius of the circle is a
The clockwise angle through which the circle turns is t
The arc k is the arc though which the circle turns as it moves from the point (0,0) to a point (N,0) on the x-axis
Let C be the center of the circle that travels from the point O, the origin, to the point N on the x-axis, then the central angle of the arc k is the angle NCP, and the length of the arc k is the distance ON.
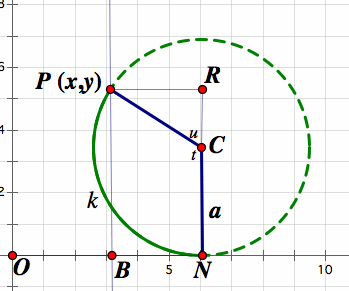
Therefore the measure of the arc k will be the product of the radius a and the angle t. Because we have established that length of the arc k is the distance ON, then at = distance ON
Since the x coordinate of P(x,y) is at distance OB = distance ON - distance BN = at - a sin t = a( t - sin t).
This is because distance BN = distance PR = a (sin u ) = a sin(-pi - t) = a [ (sin -pi) (cos t) - (cos -pi) (sin t)] = a sin t
Since the y coordinate of P is distance BP = distance NR = distance NC + distance CR = a - a cos t = a (1 - cos t)
We can also see that distance CR = a cos u = a (cos (-pi- t)) = a ((cos -pi) (cos t) + sin (-pi)(sin t)) = a (- cos t) = - a ( cos t)
Thus the parametric equations of the cycloid are:
x = a (t - sin t)
y = a ( 1 - cos t)
Constructing a cycloid in Geometers Sketchpad
In order to construct a cycloid in GSP the following steps can be taken:
1. Construct a line segment, l.
2. Mark a point A on the line l.
3. Construct a perpendicular line at A to the line l.
4. Construct a shorter line segment m.
5. Select the point A and the line segment m and construct a circle by center and radius.
6. Mark the upper intersection of the circle and the perpendicular line and select that point and the line segment m, and construct another circle by center and radius.
7. Now erase the original circle and the perpendicular by selecting them and then clicking Display, Hide objects.
8. Select an arbitrary point on the circumference of the circle (say a point C) and Click Edit, Action Buttons, Animation, Counterclockwise, medium speed.
9. Select the point where the circle intersect (is tangent to) the line l, click Edit, Action Buttons, Bidirectional, medium speed.
10. Click the arbitrary point C, then click display, trace
11. Drag the circle to the extreme left of the line l, then click the animation buttons and watch your circle trace out the shape of the cycloid.
A cycloid that is constructed in GSP and animated should give the following results: cycloid movements