Tangent Circles

By Leighton McIntyre

Goal : To construct and Investigate Tangent Circles

Assignment 7

This task will be broken down into 3 parts.

1) The first section will deal with tangent circles where one circle lies inside the other.

2) The second section deals with tangent circles where two circles are outside each other

3) the third section deal with tangent circles where two circles cross cross each other

A tangent circle is one which touches two other circles at a point of tangency.

Case 1: one circle lies inside the other

Construct two circles one inside the other. Then choose a point of tangency on the outer circle. The theorem is that the midpoint of the tangent circle will lie somewhere on the line joining the center of the outer circle to the point of tangency on the circumference of the outer circle. Construct a length on the radius of the outer circle that is equal to the radius of the inner circle, by making a circle at the point of tangency of the outer circle that is equal to the radius of the inner circle. Construct a line segment from the center of the inner circle to the point on the intersection of the line from the tangency of the outer circle to the outer section of the new circle similar to the inner circle. Construct the mid point of the line segment and then a perpendicular to the line segment. Then make the intersection of this perpendicular and the line from the center of the outer circle to its point of tangency the radius of a new circle which is the tangent circle. The blue circle center C is the tangent circle.

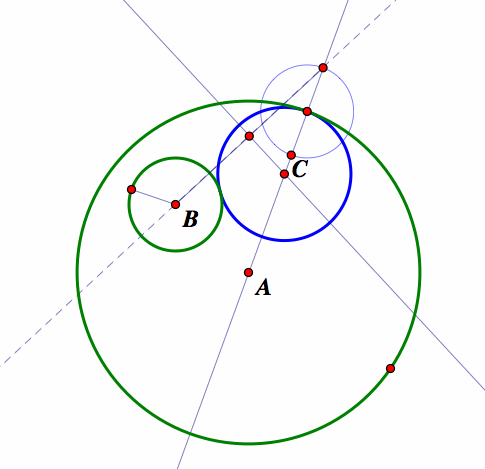
We can now construct another tangent circle to the original circles by constructing a segment from the midpoint of the inside circle, to the intersection of the line through the midpoint of the larger circle and the copy of constructed smaller circle on the inside of the larger circle. Then construct the midpoint of this segment and the perpendicular to this segment. The green circle center

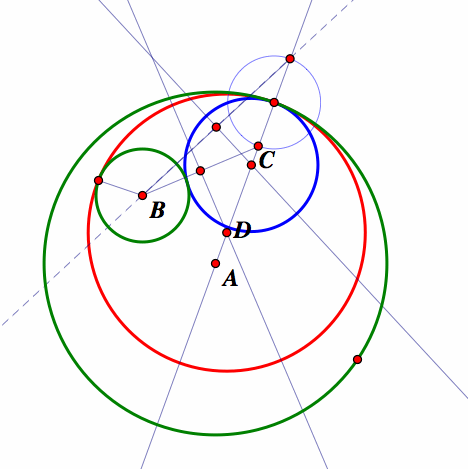
Now conduct the investigations of the tangent circle by setting the path that is traced out by the Trace points C and D, the centers of the tangent circles. Animate point to get the following.

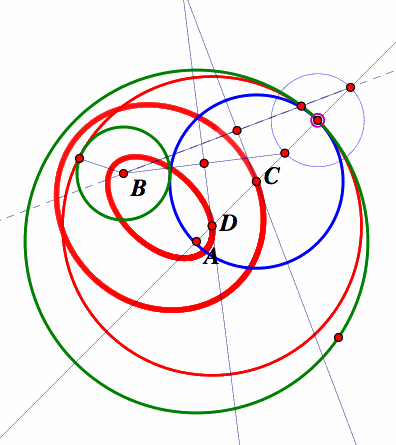Notice that the path traced out by the centers tangent circles of the tangent circles for two ellipses with foci being the centers of the original circles.

Case 2: two circles are outside each other

We repeat the construction but this time we construct two circles outside each other than construct a tangent circle to the two circles by the same process mentions in 1 above. We get the first tangent circle looking like the one colored in blue below.

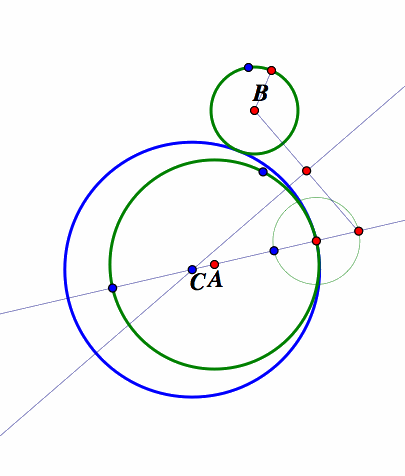
We then construct another tangent circle that encircles the two original circles by using the same process mentioned in one above for constructing the second tangent circle. We now have have a tangent circle like the one colored in red below.

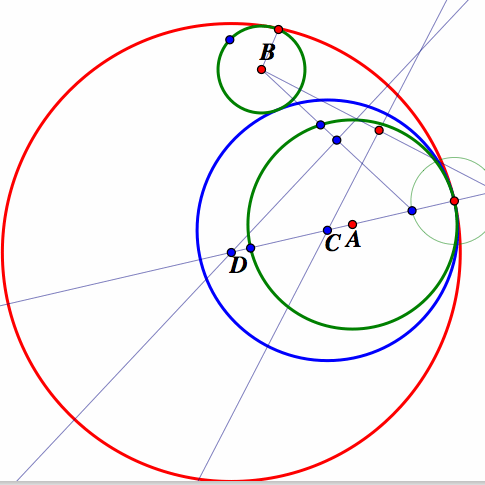
We now conduct an investigate by animating the intersection of the line through the center of the larger circle and the center of the constructed smaller circle we call point F, and observe the traced motion of the centers of the tangent circles points, C and D. The diagram below show this picture.

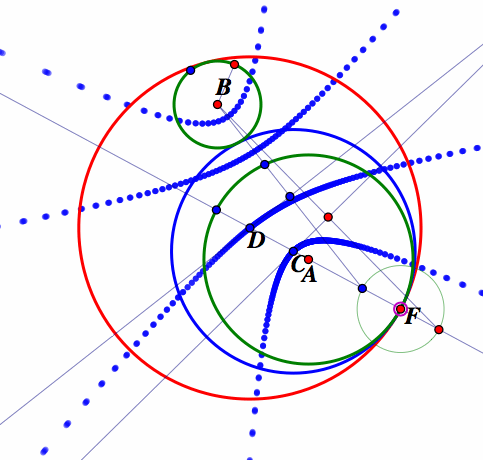Now notice that the centers of the tangent circles trace out two blue hyperbolas with the foci being the centers of the original circles, A and B.

Case 3: Two Circles Cross Each Other

We repeat the construction but this time we construct two circles crossing each other, and construct a tangent circle to the two circles by the same process mentions in 1 above. We get the first tangent circle looking like the one colored in blue below.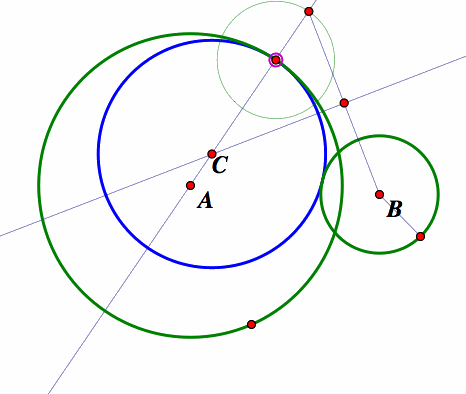

Again we construct another tangent circle that encircles the two original circles by using the same process mentioned in section 2 above for constructing the second tangent circle. We now have have a tangent circle like the one colored in red below.

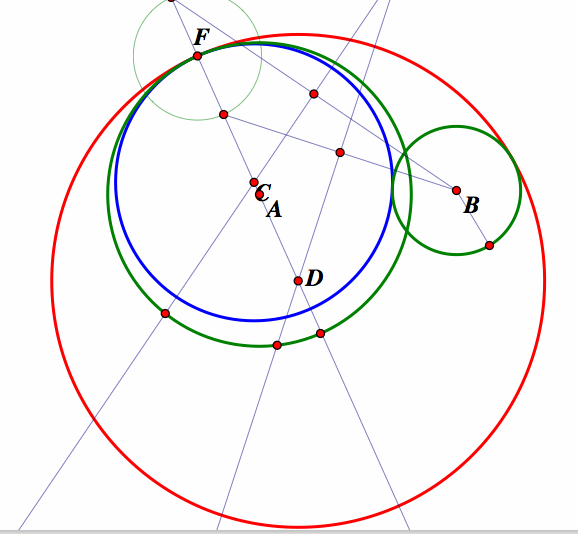
Now when we animate the point F and trace the movement of the centers of the tangent circle, C and D, we have the following picture.

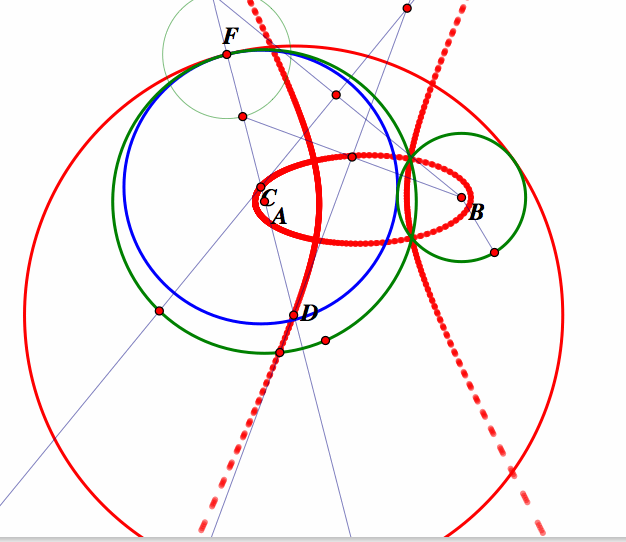
Notice now that the center of the blue tangent circle, C, traces out an ellipse, while the center of the red tangent circle, D, traces out a hyperbola. The foci of the ellipse and hyperbola are the centers of the original green circles, A and B.

Return to Leighton's Homepage.