
Assignment 1:
Exploring h(x) = f(x)g(x) when f and g are linear
by
Teo Paoletti
Goal: Find 2 linear functions f(x) and g(x) such that their product h(x) =
f(x)g(x) is
tangent to each of f(x) and g(x) at two distinct points. Discuss and
illustrate
the method and results.
As with any open
ended
problem of this type, our first thought may be to plug in some numbers
and look
at what happens. Because of that, I made a first attempt of:
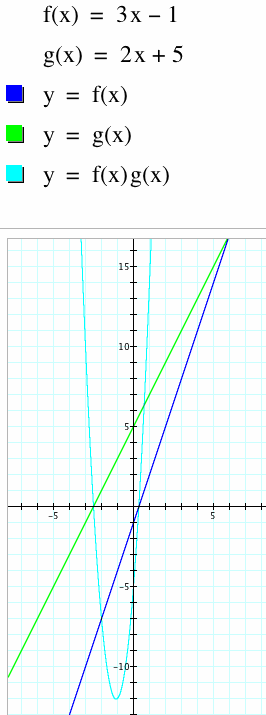
Clearly from this result, guessing
and
checking will likely be a futile effort.
My first attempts included setting up
a
system of equations and attempting to plug in values that worked. While
one
attempt was successful, further attempts were unsuccessful, showing the
futility of these efforts. Because of that I decided to take a more
computational approach (with the help of the CAS Maple).
I started with the following system
of
equations:
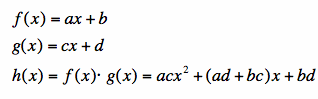
Now since I know at some fixed x, f(x) and h(x) intersect
and
are tangent, and similarly for some fixed y for h(y) and g(y), I have
the
following system of equations, where equations (3) and (4) come from the fact that f'(x) = h'(x) and g'(y) = h'(y).
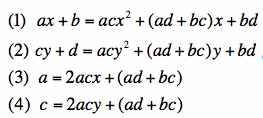
Now I began to play with Maple. First
I
solved equation (3) for x and plugged that into equation (1) elimating x. Then I solved that equation for a. Similarly, I solved equation (4) for y and
plugged it into
equation (2) eliminating y. Then I solved this equation for a. After
solving
both equations for a, I set the two equations equal (hence eliminating
a).
After doing this, I solve the equation for d, during which the variable
c is
eliminated, giving me:
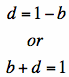
Now that I have the relationship d =
1-b, I
plug that into equations (1) and (3). Again I solve the new equation
(3) for x
and plug it into equation (1) and solve for a. In this case I get the
relationship:
a
= -c
or
a
- c = 0
Now we have a set of two parameters.
a
- c = 0
and
b
+ d = 1
When playing with these we find that
any pair
of numbers that satisfy the parameters will work as seen with the
animations
below.
Animation 1(a and c vary):
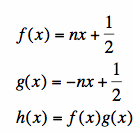
Animation 2 (b and d vary):
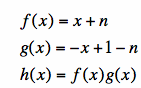
Animation 3 (all 4 vary):
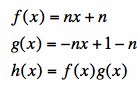
Another set of arguments on this problem can be found here. The author of this article uses a different technique to obtain the same set of equations a - c = 0 and b + d = 1. They point out that f(x) = 0 when g(x) = 1 and g(x) = 0 when f(x) = 1. However, my animations go one step further to show that f(x) + g(x) = 1 for all x (not just when one or the other equals 0 or 1). Another observation that can be seen from this article is that the point of intersection of the f(x) and g(x) is always at y = 1/2.