Exploring
Quadratics From a Different Perspective: Using Alternative Planes
By: Teo Paoletti
The x-c Plane
We initially look at the
equation 
. The
graph is
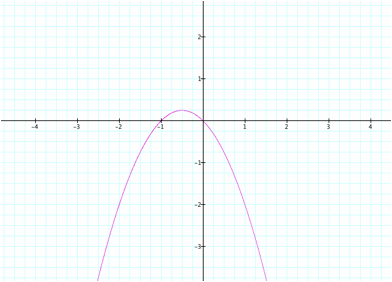
We can see that the graph is
simply an upside down parabola.
This makes sense as we can transform our function to be 
. Hence
the zeros of our new function are x = 0 and x = -1. Since the equation in the x-c plane has only an x-squared and x term, our graph will
only stretch or shrink according to the value of b. The zeros will always correspond to x =
0 and x = -b. We can see this in
the animation below.
The x-a Plane
We first look at the x-a
plane through the graph of
. Unlike
the x-c plane which also
gave us a parabola, this plane provides a dramatically different picture.
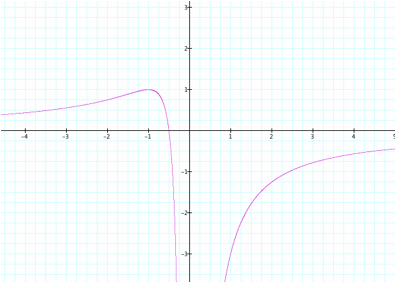
The graph appears to approach
0 and x goes to infinity and negative infinity. The graph seems to have a maximum around
-1, and a vertical asymptote at x = 0 (although we would need a zoomed out
picture to see that). The graph
also appears to only have one zero at x = - ½ . The zero is easy to explain, because if
a = 0, the equation simply becomes 0 = 2x + 1 which has a solution of – ½ . The
horizontal asymptote can be explained by the fact that if x = 0, weĠd have the
equation 0 = 1, which is a contradiction.
Hence the graph does not exist at x = 0. It is worth noting that if we were to
eliminate c, and graph 
, then when x = 0, weĠd have 0=0 which is true. However, there is still a vertical
asymptote at x = 0, but now the two sides go in opposite directions.
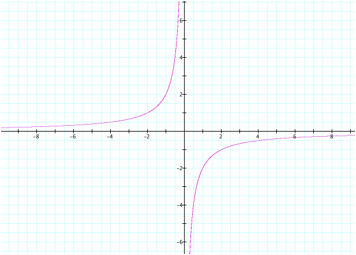
This graph makes sense though
because if we were to solve 
we get 
.
Now going back to our
original graph, if we insert the line a = -1, we see that the line crosses the
graph at exactly two points. We
realize that these two points would correspond to the solutions of the equation
.
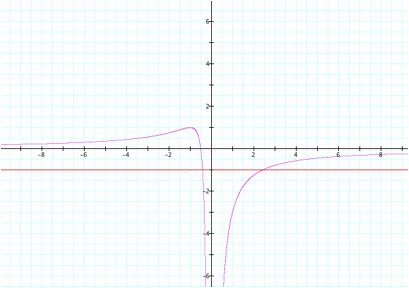
Similarly if we slide the
line y = n up and down we see that the line crosses the graph at either 0, 1, or 2 places. If n > 1 the lines never intersect,
meaning there are no solutions to our original equation. If n = 1 or 0 then there is only one
solution to our original equation.
And if 0 < n < 1 or n < 0, then there are two solutions to the
original equation. Hence we can use
the x-a plane to explore the zeros of our initial equation as well.