
Assignment 7: Tangent Circles Exploration
by Teo Paoletti
Goal: My goal in this assignment was to put myself in the position of a high school geometry/algebra 2 teacher who wants to use GSP to introduce the properties of ellipses in his class. In doing so, I had to think as both student and teacher to make sure the activity was manageable but also explored deep mathematics.
In trying to create a lesson exploring the properties of an ellipse, I would first either have the students construct a circle tangent to two other circles (if there is time) or have the script already loaded onto their computers as to allow them to utilize the script.
I would begin class by having students draw a large circle and then a second circle completely contained in the first using the GSP script tool tangentcirclesatapoint. I will ask the students to manipulate the point on the larger circle to see what is formed by the locus of centers of the tangent circle. For instance, one could look like this:
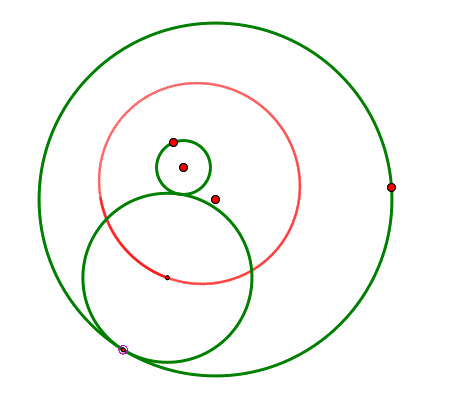
Because of this, students may initially conjecture that the locus of points would form a circle. To challenge this idea, I ask tell students to explore various positions and sizes for the interior circle to make sure their statement about circles is true. Hopefully they will see pictures that look more like this:
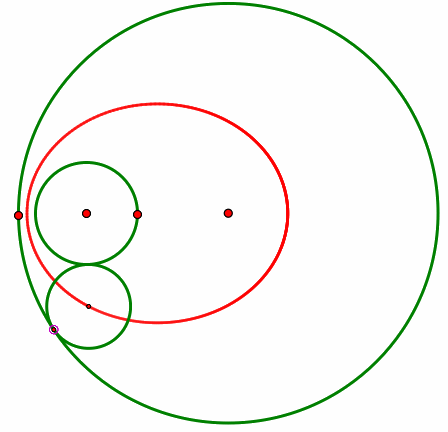
At this point, I would expect students to say that the shape is not always a circle, but it is atleast always an oval. Once all of the students have generalized this far, I would ask them to draw a line segment from the center of each circle to the center of the tangent circle, as pictured below.
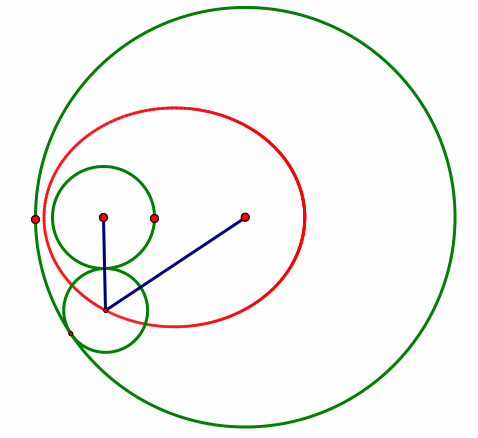
Then I would have them animate the graph again, paying attention to the lines and asking if they notice anything. Some answers I would expect would include the fact that as one line segment grows, the other shrinks. I would also expect students to say that each segment has a minimum and maximum length achieved at the 'long ends' of the oval. I may also expect them to say that the line segments appear to be equal at the 'short ends' of the oval. I would be curious to see if any other patterns emerge from student thinking that even I am not noticing!
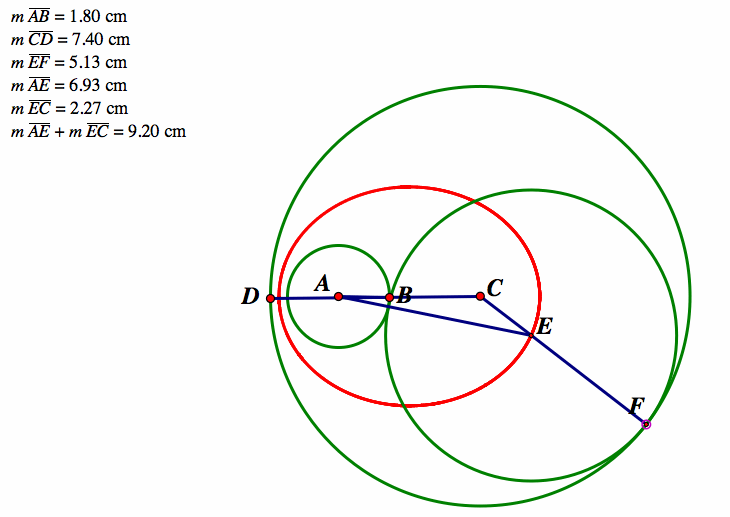
After establishing the inverse relationship, I would have the students use GSP to measure some lengths in the picture, including the length of radii of all 3 circles, as well as the length of both segments as shown below.
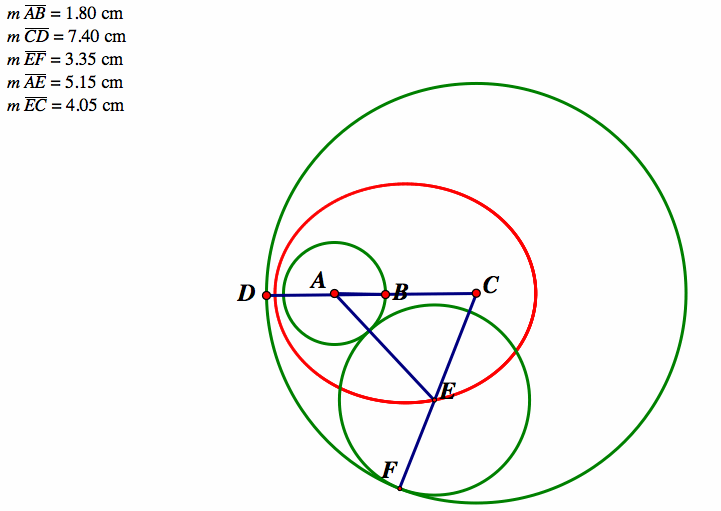
I would ask the students to explore any relationships they see in the numbers as they animate the graph. I would expect the students to observe that two of the radii remain constant, while the other three lengths all vary as the point moves around the larger circle. I would ask my students to explore the minimum and maximum lengths they conjectured about earlier, as well as the instances when the lengths appear to be equal. For example, in the graph shown above, one line segment has a minimum length of 2.10 cm when the other segment has a length of 7.10 cm. When we move to the other side, we see the same measurements but on opposite segments. (Shown Below)
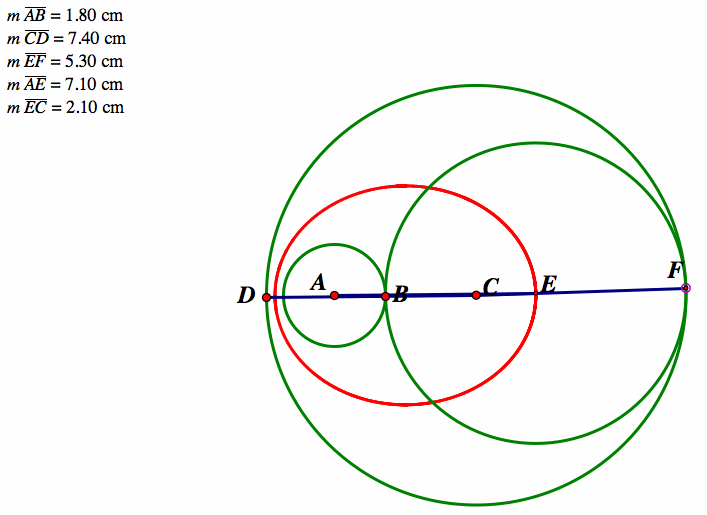
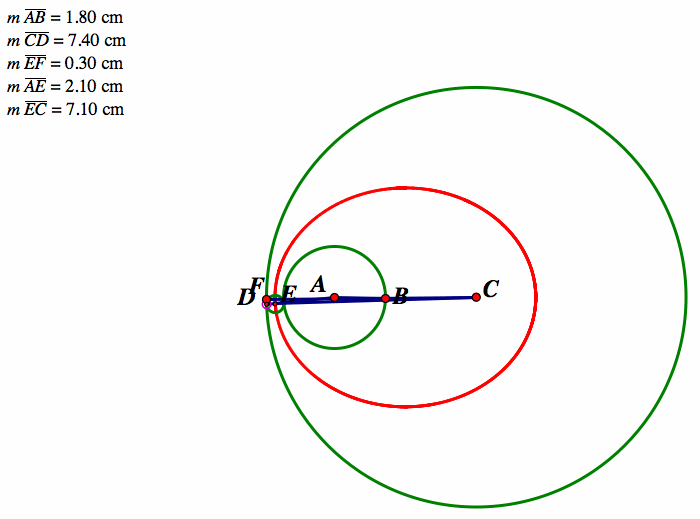
Depending on if the students conjectured that this segments would be the same on both sides, this may come as a surprise to some students, especially since the radius of the tangent circle goes from 0.30 cm on one side to 5.30 cm on the other side. This will hopefully begin to establish the idea that the two line segments have a relationship. Next I would have students find the times in which the two line segments are equal. On one side both segments have a measure of 4.60 cm while the radius of the tangent circle is 2.80 cm. On the other side, we have the exact same measurements (radius of tangent circle and all)!
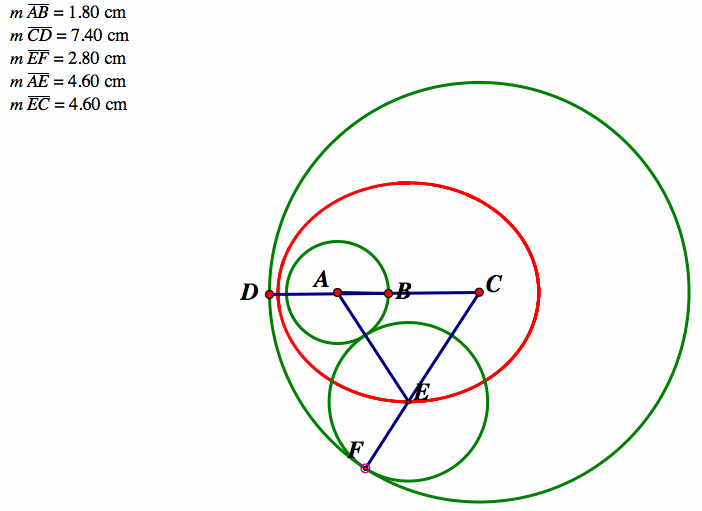
From here I would ask students to look at all of the different pairs of lengths of segments to come up with any conjectures. If they are struggle, I would tell them to make a chart with Segment 1 Length and Segment 2 Length as headings then writing ordered pairs of lengths they find in the chart. For our example:
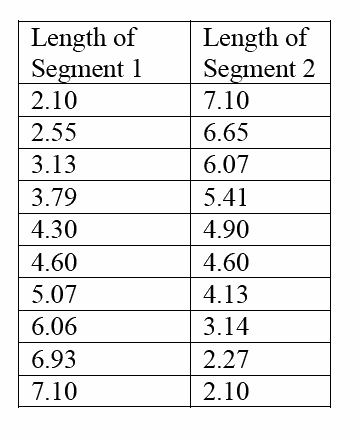
First I think students will notice that the decimals always seem to have hundredth digits that add up to 10. Having them extend this idea to see what happens beyond the hundreth digit, students will notice either quickly, or after making the chart, that the sum of the length of the two segments are always equal to the same number, in our case 9.20. I would have the students use GSP to calculate this sum, and animate to ensure that they are seeing a constant relationship.
After doing this, we can begin to introduce formally terminology. We can define the 'oval' to be an ellipse and the centers of the two circles to be foci. We can also give the property that sum of the distances from each point on the ellipse to each foci is constant. In doing this activity, hopefully I have given my students a chance to construct the idea of ellipse, foci, and properties of ellipse for themselves and help them achieve a deeper understanding of what an ellipse actually is. This activity could lead into a more formal discussion of other properties of ellipses, as well as the equations of an ellipse (a topic that can be quite dry on it's own!).
Here is an html applet that allows you to show that the measure of AE and CE always sum to the same number.
The great part of this exploration is that after we complete our work exploring the properties of ellipses, the next thing typically in a curriculum is hyperbolas. When introducing hyperbolas, we can go back to this same applet and explore further. This time, I will ask my students to move the two circles are no longer within one another nor intersecting at all. When they do this, the following picture is produced by tracing the center of the tangent circle:
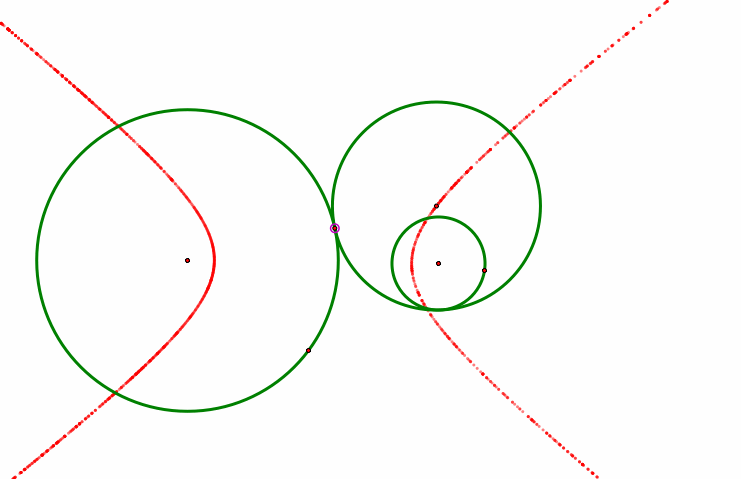
We could then use this picture to develop the theorems and properties of a hyperbola.
Hopefully by building the hyperbola introduction from the ellipse introduction, students realize implicitly that there is a relationship between the two figures. This may be extremely helpful in the overall exploration of conics and these figures can often seem unrelated to students.