
Assignment 9: Exploring Simson's Line
by Teo Paoletti
Goal: Find all conditions in which the three vertices of the pedal triangle are colinear (that is the degenerate triangle).
We start with any basic triangle along with its pedal triangle.
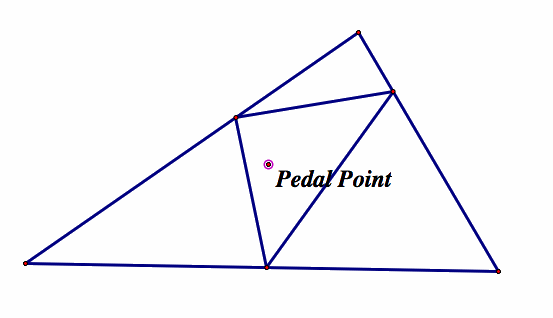
As we explore, we first find that at each vertex, the pedal triangle degenerates:
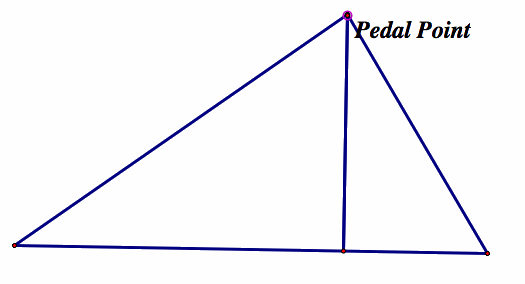
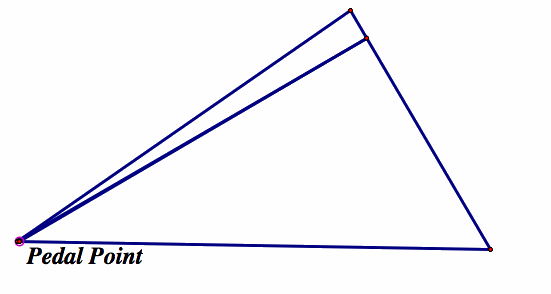
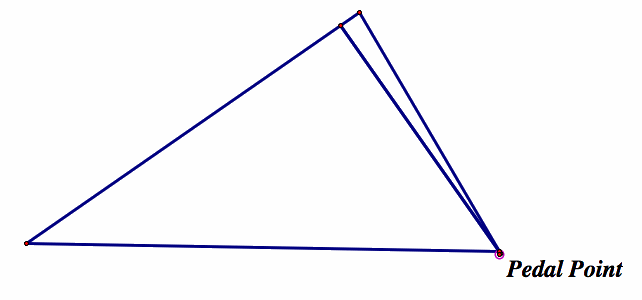
So now our instincts may tell us that since the verticies work, any point on the triangle itself may work. However, looking at what is produced:
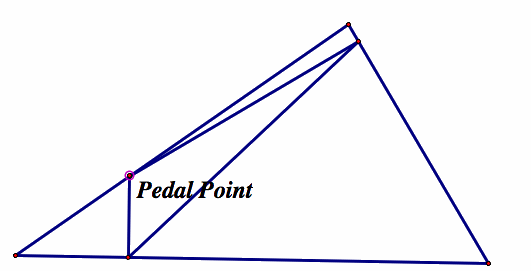
It is plain to see that our intiution has misled us! Moving the point all around the triangle and inside the triangle, we see that there is no location besides the verticies where we have a degenerative triangle. Does this mean the verticies are the only points? We continue to play around and begin to find some points on the outside of the triangle that work!
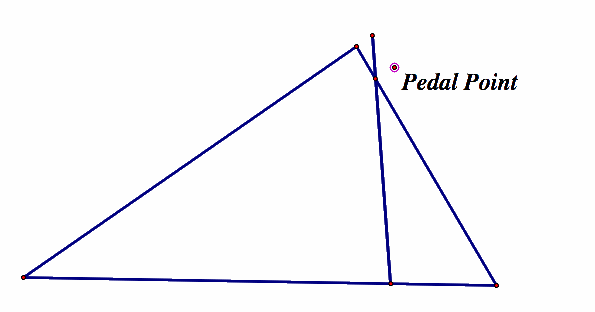
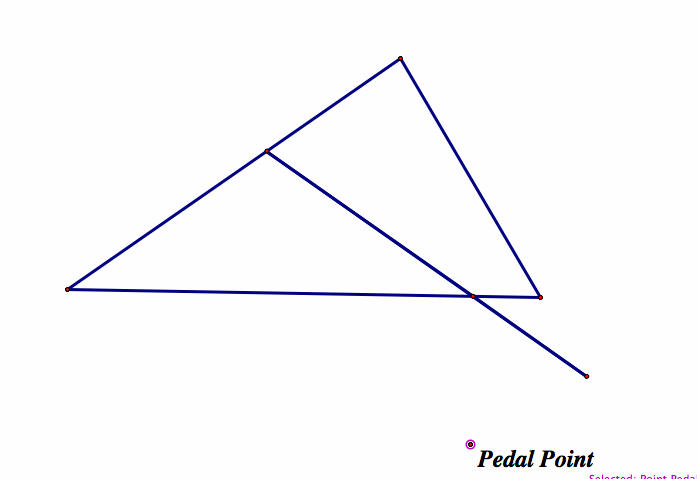
Playing with these, we begin to see that if we are careful about how we move the point, we can keep this degenerative triangle. Furthermore, there seems to be a pattern to where the point needs to be. Clearly we need to go through all 3 verticies and it seems that we are tracing a circle when we try to keep the degenerative triangle as we move around. Because of this, we decide that we should explore the circumcircle to see if there is a relationship. Drawing the circumcircle, we get:
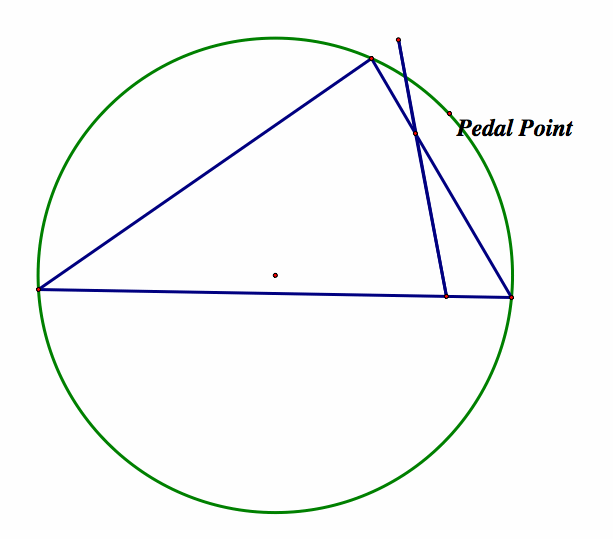
So far our conjecture about the point being on the circumcircle looks good. Moving the point away from the circumcircle we get the picture:
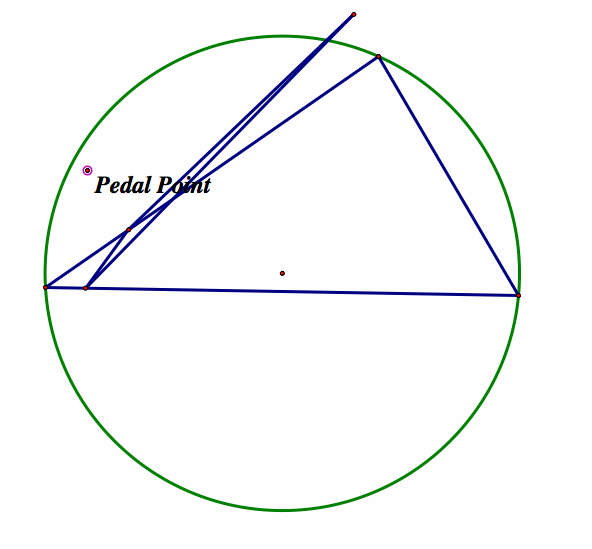
Which bolsters our ascertation that the pedal point needs to be on the circumcircle. Merging the pedal point to the circumcircle and animating, we get the following which you can find by clicking here
and hitting the animate point.
The degenerative line is called Simson's Line.
One interesting observation is that for each side of the triangle, at some point, the Simson line completely overlaps the side of the triangle. To find the point where this happens for a given side, we need to find the lines perpendicular to the two endpoints of the segment we are triying to overlap, and the other sides of the triangle as follows:
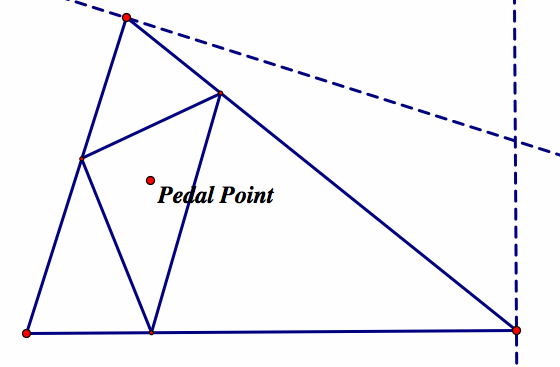
Moving the pedal point to the intersection, we see that the triangle degenerates:
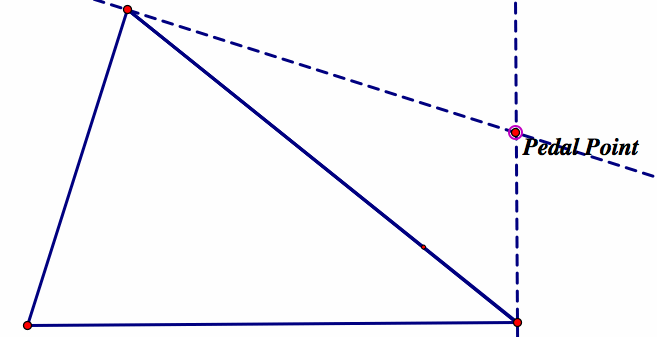
Here is an applet which shows the 3 intersection points discussed above. You can move the pedal point to each of these points to see how the triangle degenerates into a line that overlaps a side of the triangle. Further, the Show Circle button shows the circumcircle which can let you play with moving the point around the circle yourself to investigate how the Simson Line changes as it moves around the circle.
We can extend this investigation even further by extending the lines of each side of the triangle while continuing to observe what happens when the pedal point moves around the circumcircle. The applet below allows you to first move the pedal point around the circumcircle. As you see the 3 verticies of the pedal 'triangle' (in quotes because in this case the triangle is really just a line) are always one one of the lines (not just segments) of each side of the triangle. Further, while it may not be obvious, if you opt to choose Show the Perpendiculars on the applet, you will see the perpendiculars from the pedal point to each of the verticies of the pedal 'triangle.' If you continue to watch this pedal point move around the circumcircle, you will see that the perpendicular lines from the pedal point to the verticies of the pedal 'triangle' are all perpendicular to the lines that form the sides of the triangle, another very interesting observation!