This is the write up for problem set 2. We are focusing on second degree equations for this problem set. Generally they graph as parabolas but their are many interesting translations we can find by changing the coefficients of the a,band c terms respectively. Although standard form is not in a form that can readily classify the translations as you could achieve by completing the square and finding the vertex (h, k), nonetheless there are still many interesting observations we can report. From that we can explain the underlying mathematics that is applying to these transformation.
I chose to write up question # 4 In it we were asked to make the graph of the parabola 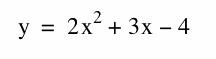
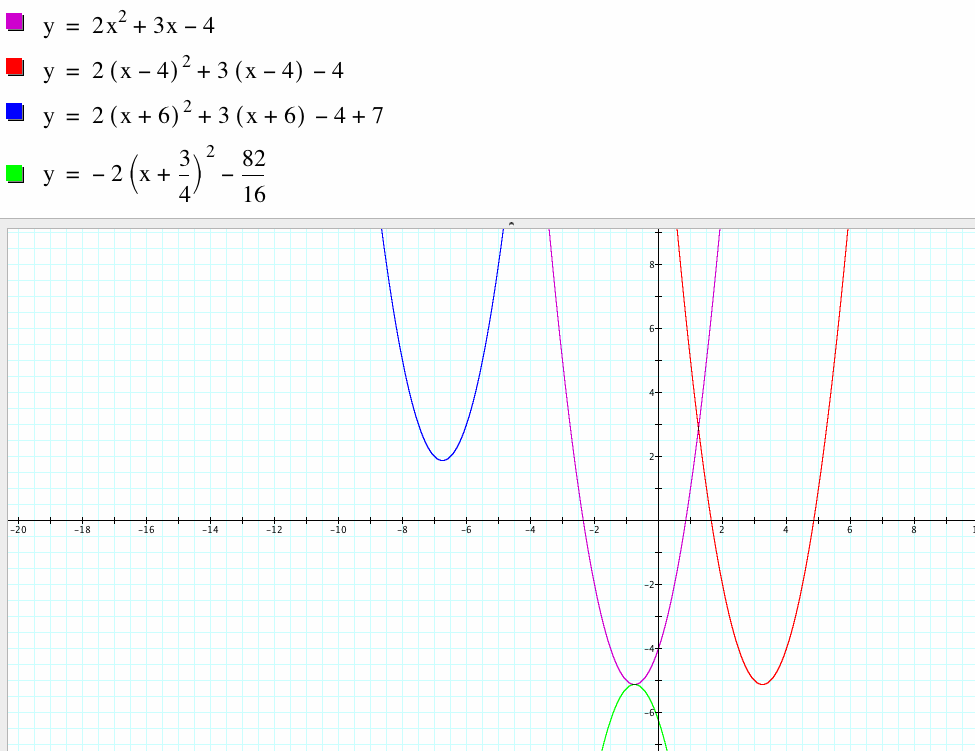
Then we overlaid each graph replacing x with (x-4). Let us explain the mathematics involved after viewing the results.
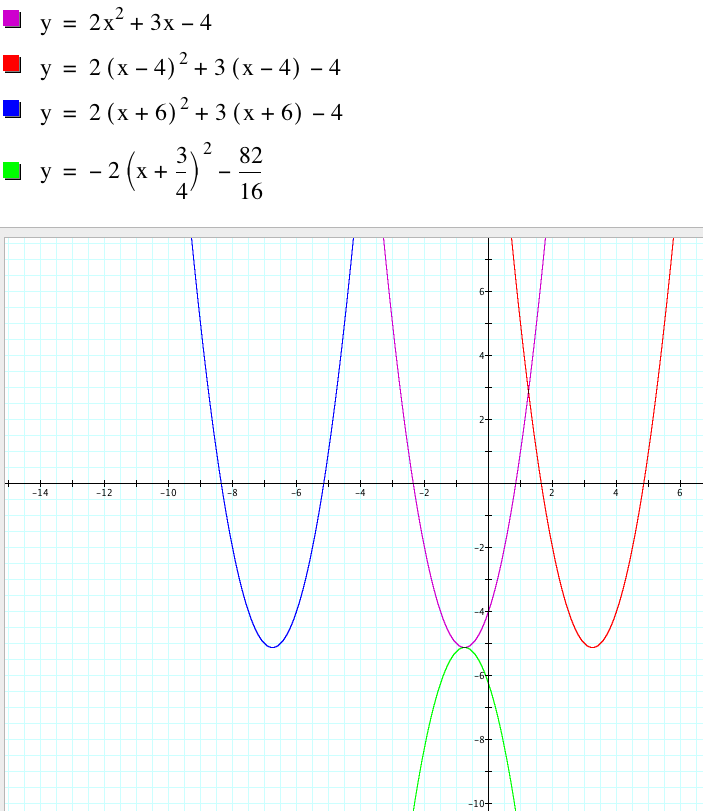
The initial function had a=2, b=3 and c=-4. Depicted by the flush graph, the graph has two real roots. You could've this with the quadratic formula, since the discriminant b squared minus four ac would equal to 41. This also indicates that while the roots are real, they are in fact irrational. This result can be verified with the quadratic formula which can be proven algebraically using a, b,and c and completing the square.
Next we investigated replacing x with (x-4) in the equation This actually had the effect of translating the graph 4 units in the positive direction. As we will see this is a common theme for parent functions the the horizontal shift is in fact the opposite of what is written in the equation. This to move the vertex of the graph to the second quadrant we made the horizontal shift (x +6) and t hen to move it up we changed the constant from -4 to + 3
To create a reflection of the original parabola reflected down across the axis y=-82/16, I calculated the vertex of the original equation by completing the square and factored out the two coefficient and simply made that negative. To generalize, we looked at horizontal, vertical translations and reflections. They can move the graph anywhere you want on the Cartesian plane, and with simple algebra like completing the square and the quadratic formula, you can obtain these results mathematically.