This is the write up for problem set 3. I have to admit the derivation of the formula for the locus of points as b is changed left me in the dust. I think I needed a few intermediary steps to be able to put all of the pieces together. I would be interested to see how it is done with calculus. Although as I think about it the first derivative would give one the instantaneous rate of change of b with respect to x and y. Here is the problem:

Some nifty algebra reveals that we are able to depict the nature of the roots by examining the xa, xb and xc planes. That is we can determine the nature of the roots over a set of domain values. First we will look at the xb plane. In this the y variable will be substituted for b in a standard quadratic equation.

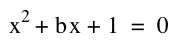
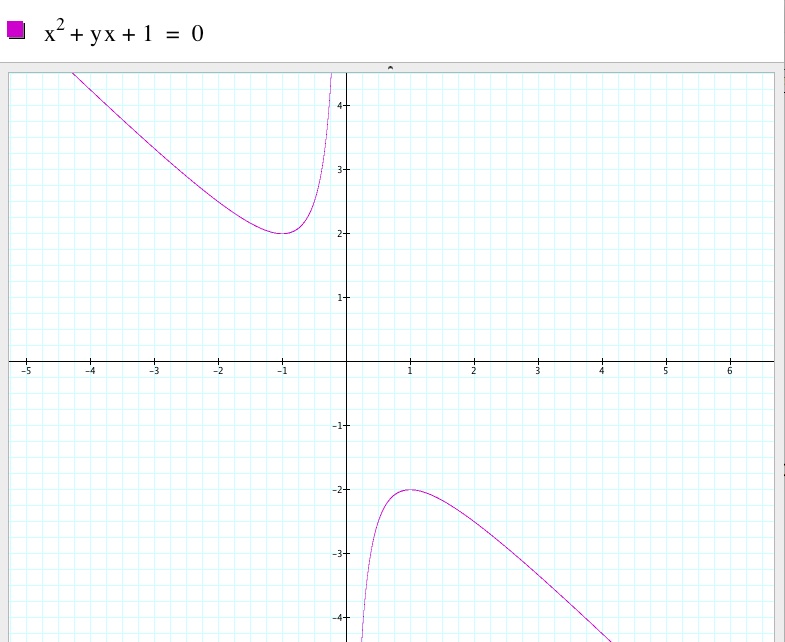
In this depiction as x approaches zero from both negative one and positive one Y approaches undefined, or conversely as y approaches undefined x approaches zero. The reason mathematically that these XB graphs are useful is to determine the number of real solutions a mathematician might find given different values of b for the original equation where a is 1 and c is as well. Of course it would also be a simple matter to evaluate b squared minus 4ac (the discriminant). If the discriminant is positive you will have two real roots. If it is zero you will have one real root; negative b over 2a, and if it is negative you will have no real roots which in this depiction of the xb plane is the void from about two to negative two.

RETURN TO ROBERTSON HOMEPAGE