
EMAT 6690 Essays
by Brent Robertson
Essay One. The use of MATH TUTOR software versus other technologies for student self studies of conic sections in grade 11.
I was interested in exploring the idea of computer assisted learning from early on at my studies at the University of Georgia. My first degree here was a Specialist in Instructional Technology. At the time in 2007 I purchased software from MathTutor Educational Software. This software was developed in Indiana (and from my phone contact in the ordering process it was acknowledged that there was some collaboration with Purdue University, however any association with Purdue is not mentioned on the web site. According to the company, "The Math Tutor software is ideal for students, teachers and parents because it is a proven curricular based software for grades 6-12." According to the publisher, Math Tutor utilizes dynamic graphics and animation to enrich understanding of fundamental mathematical concepts These dynamic tools help students gain a strong understanding of fundamental math concepts. The software is said to be ideal for self-study and home school students who work at their own pace one step at a time.
I want to look at the Math Tutor software for a given attainment, and compare it to technologies like Geogebra, Geometers Sketch Pad, and Graphing calculator to see how they go about helping students understand a mathematical concept. The mathematical concept I will use is conic sections. I choose conic sections because it is what we are learning currently at Norcross High School in Integrated Algebra 2.
Here is how Math Tutor approaches the unit:
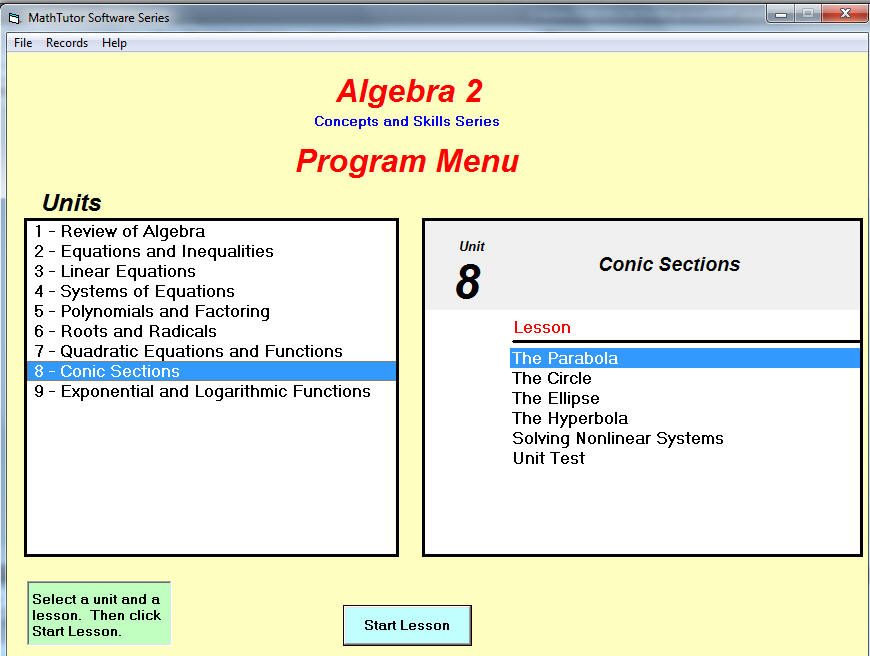
As you can see the start screen is similar to a textbook. The units are given, and by clicking a unit you will get what was normally in the table of contents for a typical Algebra 2 textbook. I want to mention here that the software is divided into to groups for each curriculum level. One is the Concepts and Skills series and the other is the Practice and Review series. This essay will utilize the Concept and Skills Series.
Geogebra will greet a student with something like this:
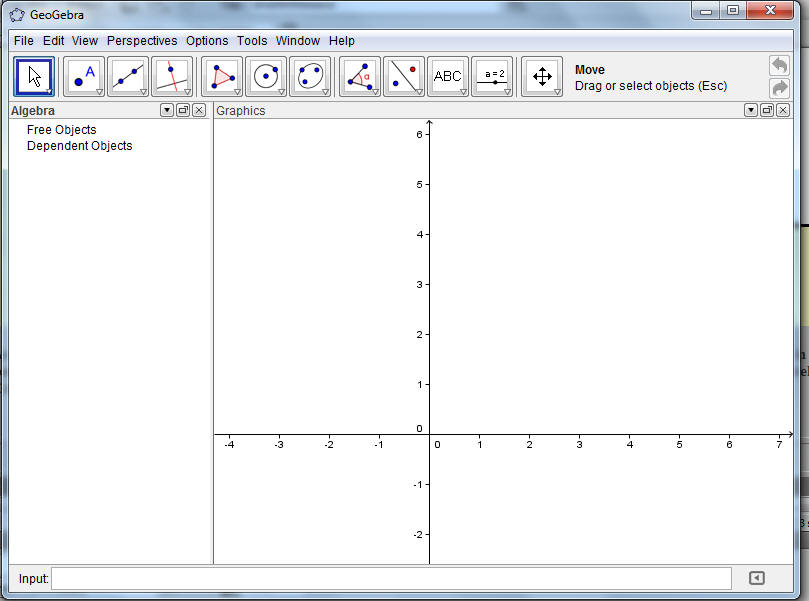
Geometers Sketchpad starts with this:
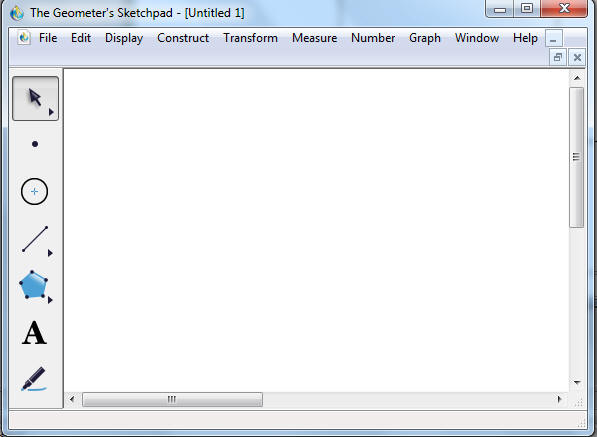
Graphing Calculator starts with this:
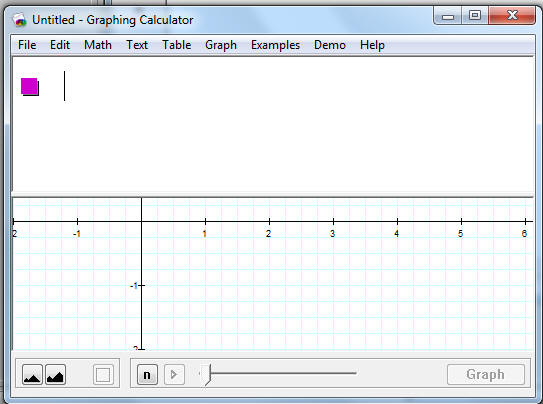
I believe that the Math Tutor software appears less intimidating to a first time user, but at the same time less sophisticated in its technology and graphics. As we will see as we move ahead the three more modern software, Sketchpad, Geogebra and Graphing Calculator have a greater learning curve as far as leaning how to use the software, but ultimately can provide a much greater depth of understanding than Math Tutor.
Math Tutor uses a sequential algorithmic approach to solving conic section math problems. In other words you could learn some procedural steps to answer questions pertaining to the concept. Here are a few examples:
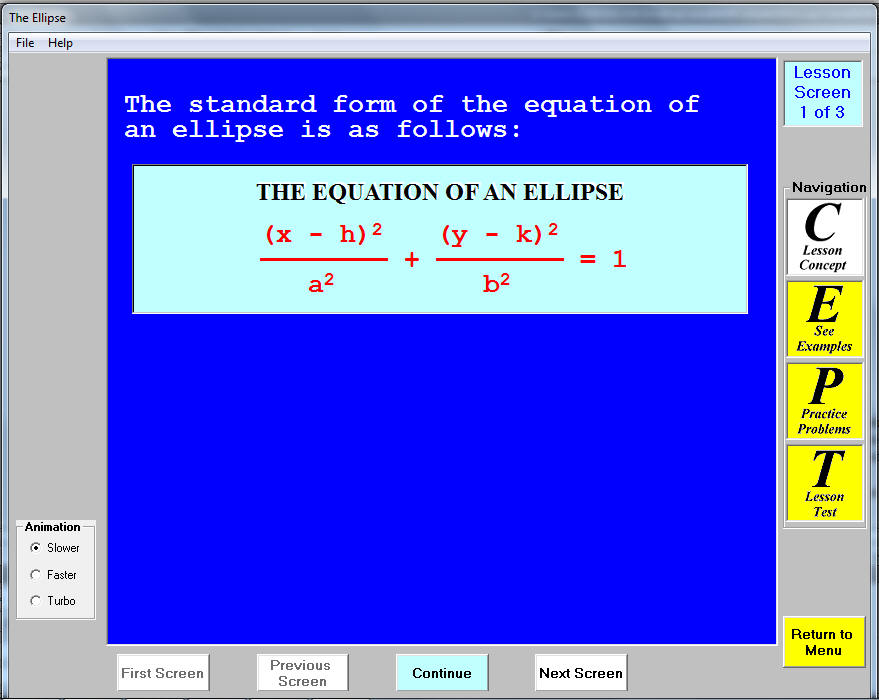
The first screen gives the standard form for the equation of a translated ellipse. The continue button urges the students to press on.
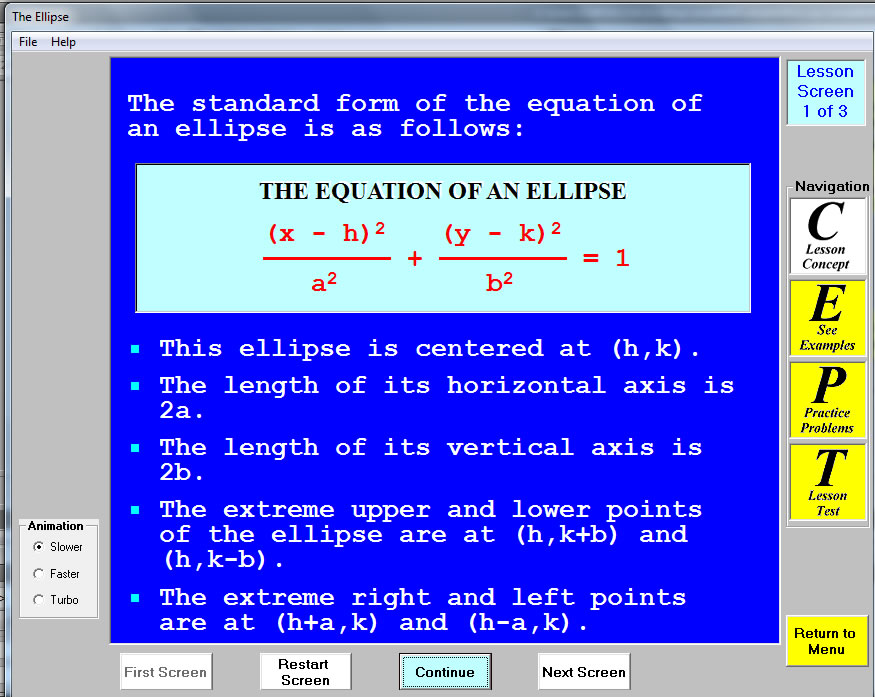
Five presses of the continue button provides five bulleted points with respect to the ellipse. Clearly some vocabulary is required by the student. Major Axis, Minor Axis will be covered with a diagram. Although the next screen doesn't include that vocabulary.
With Geogebra, a student may investigate the ellipse by following the instructions to select two foci and one point on the ellipse:
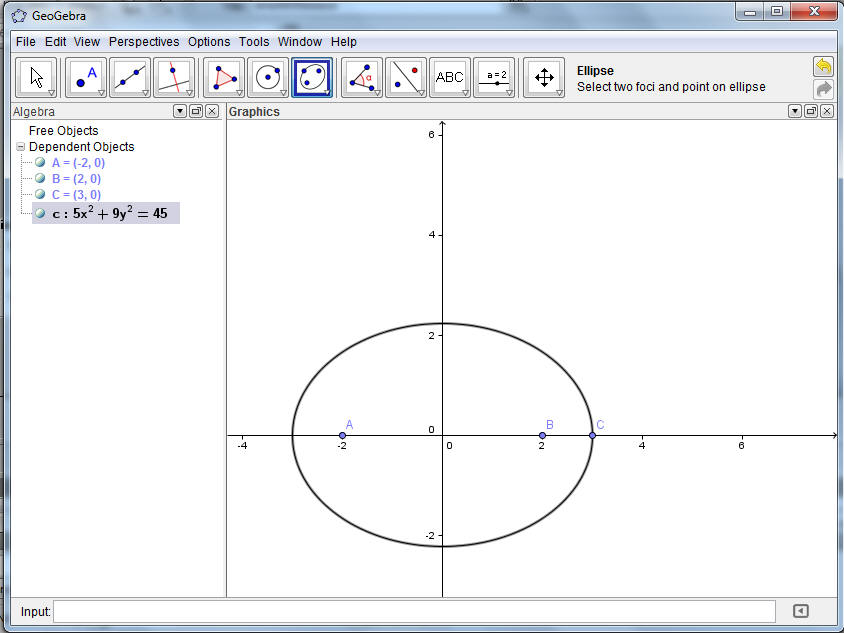
You notice that a non standard for of the general equation is given 5x squared plus 9y squared equals 45. The student will still need to put into standard form by dividing each term by 45. However what is much more dynamic is how the student can take the same graph and pull and drag points and see how the equations change and the shape of the elise changes as well:
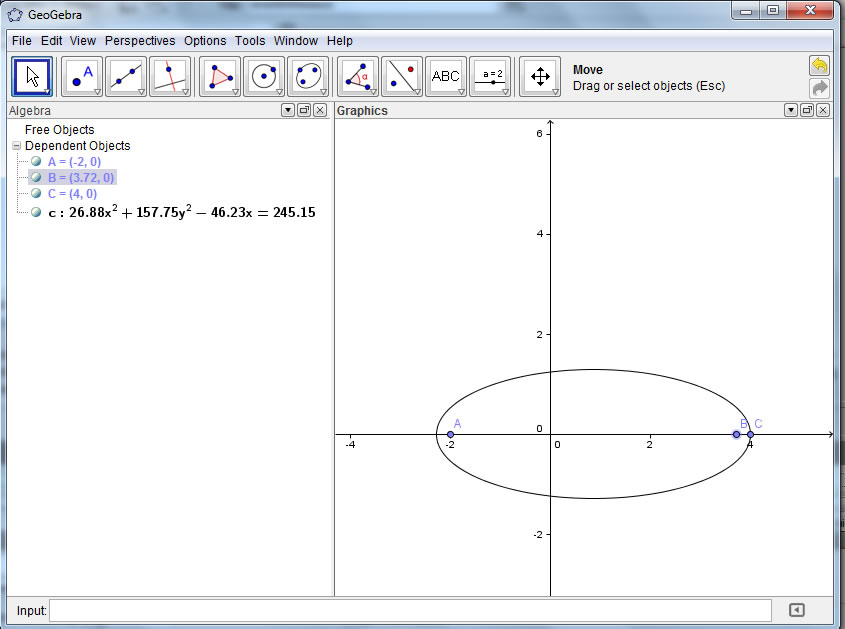
The only problem is on this graph, I put the points on the x axis. They wouldn't come off. Also some of the equations may confuse students more than they help. For example, in this diagram, the square has not been completed, so the center is not clear and the given equation may confuse students at this juncture. I can say that by experimenting further, you can start to develop so nice applications with the Gealgebra program that might be suitable for gifted and honors students. For example in the diagram below, you might pose a question such as, "Given point C is on the ellipse and A and B are foci, locate your foci in a position such that the standard equation comes out 'nicely'.
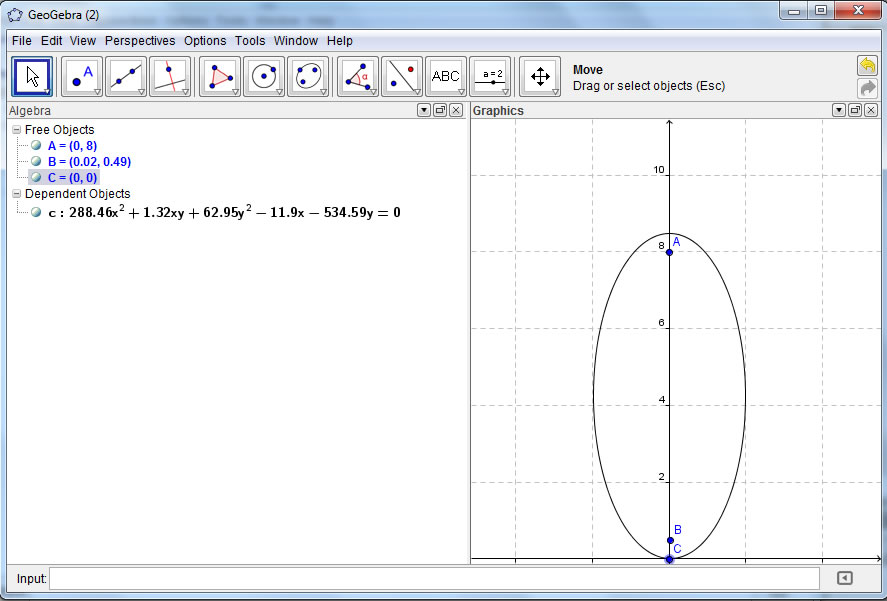
The honors student would probably try to locate the maximum point on the ellipse at (0,8). Then some calculation involving the relationship between the major axis 2a and the minor axis 2b and the distance from the center, c where "a" squared minus (for an ellipse) "b" squared equals "c" squared. Some manipulation of the points could yield a solution so that if the point on the ellipse, point C is located at (0,0). Then if the student wanted to get some nice numbers, they could substitute h, k plus and minus c where c is an integer, but really they don't need a friendly number for c , they need a friendly number for a and b. Working from a "Center" they could call the co vertices h plus and minus b and vertices k plus and minus a if they wanted a vertical major axis and h plus or minus a and k plus or minus b if they wanted a horizontal major axis. Plus you could introduce the problem of "canted major and minor axis, although this would do nothing for you in terms of finding friendly integers for the coefficients of the equation. So Gealgebra has a lot of mathematical potential, but for standard algorithmic learning at a lower level the Math Tutor program may be more appropriate.
Now let's look at how a student might generate some understanding of the conics with the ellipse:
This is the basic equation as it would appear in a textbook with a and b equal to one
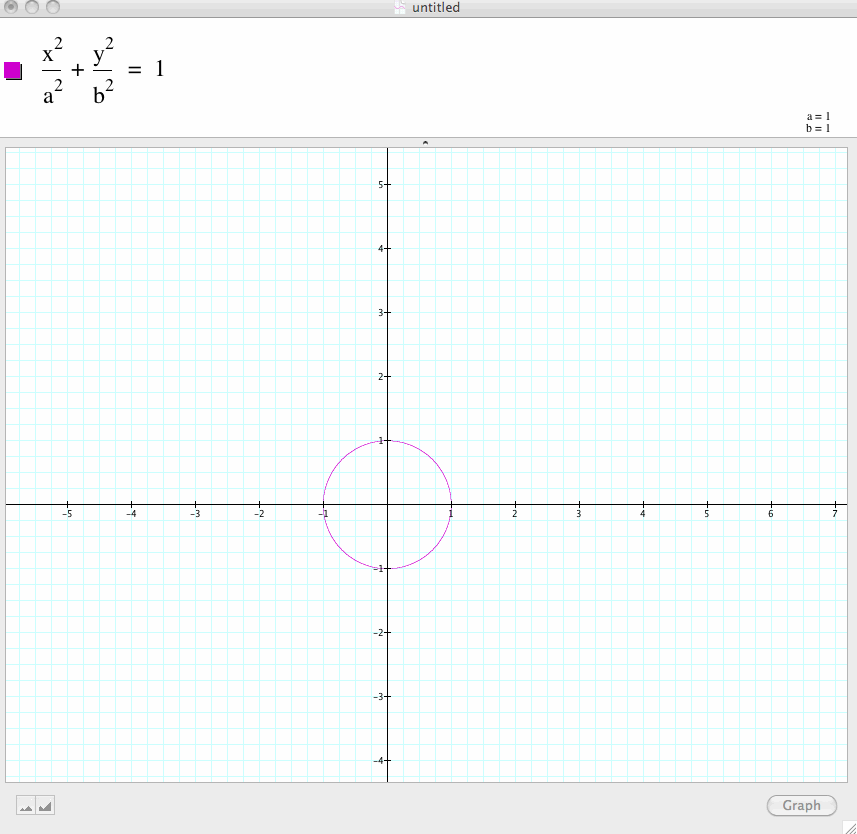
Changing a and b yields the major and minor axis.
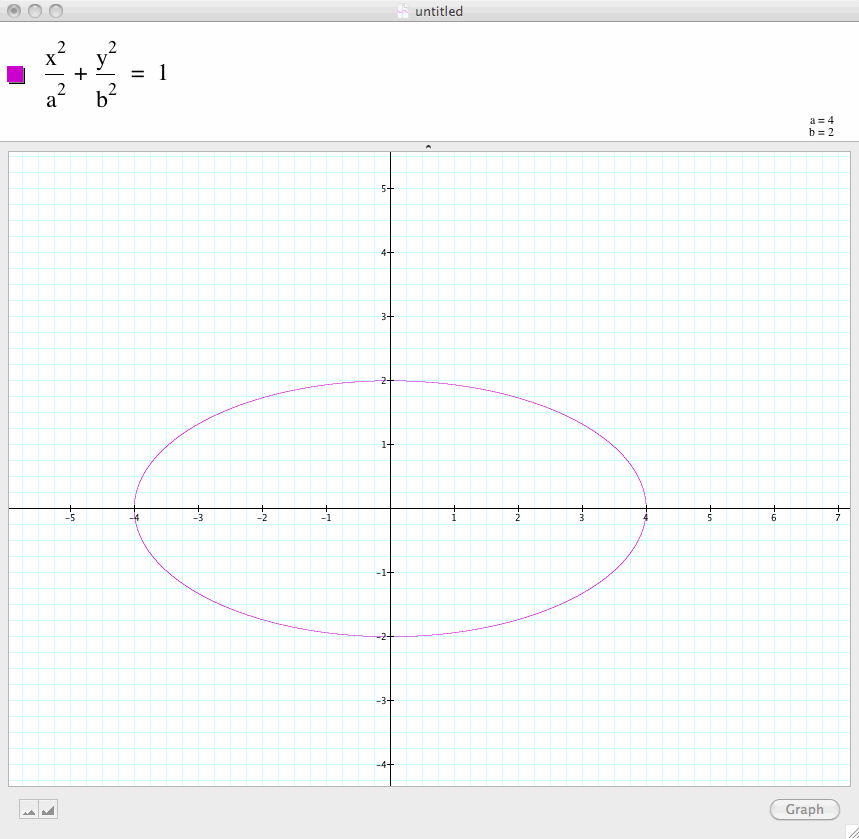
Or make the vertical axis 18 with a=9 and h=3 for a horizontal translation:
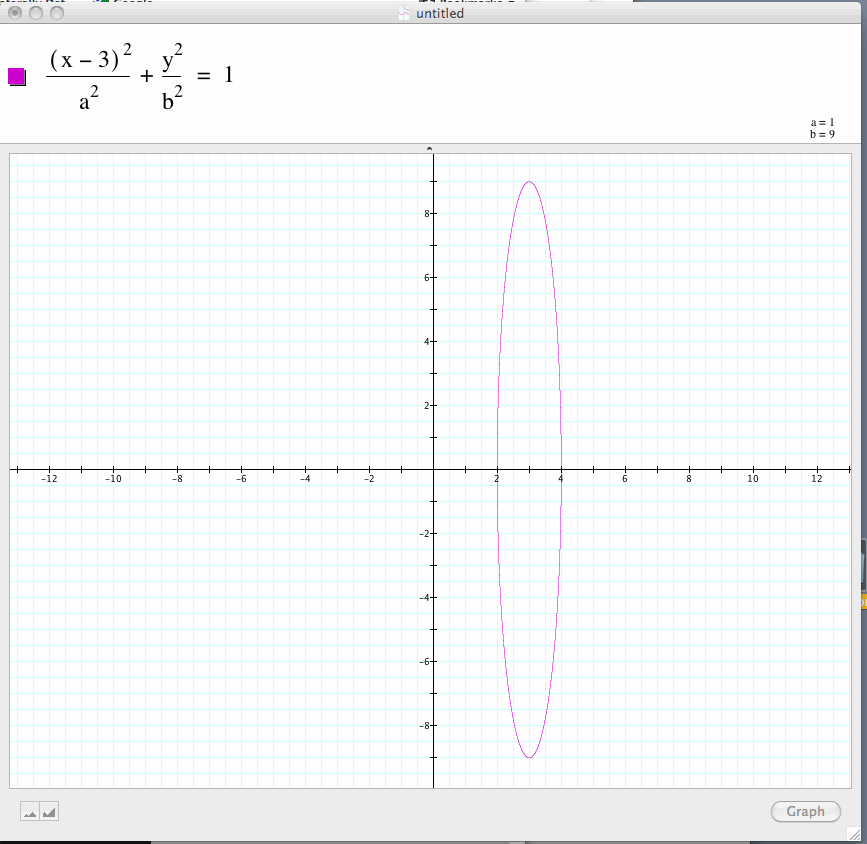
Another advantage of the graphing calculator is the ability to see conic graphs change dynamically by adjusting the parameter which graphing calculator calls "n". Here is an example of an elipse just as graphed above, but with changing the a value (we'll call it n) between 5 and 1.
Can the student perform the algorithmic computations required to do well on standardized criterion referenced math exams? For example locate the vertices, co vertices and foci of the ellipse. Although the program is extremely creative, locating key points that may be assessed on a test is not as straight forward as the Math Tutor program even with its outdated graphics. so where does that leave us to do with Geometers sketchpad? Well there is one very nice application that deals with the formal definition of an ellipse, that can be accomplished nicely with gsp this is the location of two foci and maintain the locus of all points that are a fixed total sum distance from the two foci. Here is how this is accomplished:
Follow these construction parameters> First construct a line segment AC with a point called B between A and C. The length of AC will be the constant sum that makes up the definition of the ellipse. Each circle that we construct with one foci as its center will have either AB or BC as its radius. Although we will animate the point B across the segment AC the distance of AC will remain constant. So the sum of the radii of my two circles will be a constant sum, and when we trace the intersections of the circles, which will give us the sum of the radii, we will get our ellipse. This type of exploration would not be possible with Math Tutor. Again the dillema remains, this is a great conceptual tool, but can the student get the rigor and practice to calculate, vertices and covertices, foci, major axis, minor axis and a and b that they will need for standardized tests of achievement? In this case, the MATH TUTOR software may be advantages.