by Brent Robertson
Many students are encouraged to take rigorous courses in high school with the competitive nature of college entrance requirements. Perhaps the most rigorous level of high school courses is the so called AP or advanced placement. These are considered to be college level courses, and as such, if a student is able to pass the AP exam, in many institutions they will be granted college credit for their achievement. Their are currently three mathematics AP courses being offered: AP Statistics, AP Calculus AB and AP Calculus BC.
There are several opportunities to use technology as a means to pass the exam. We shall explore these in this essay.
One of the best ways to prepare for any test is to take practice tests.
Here is an example of what the internet has to offer:
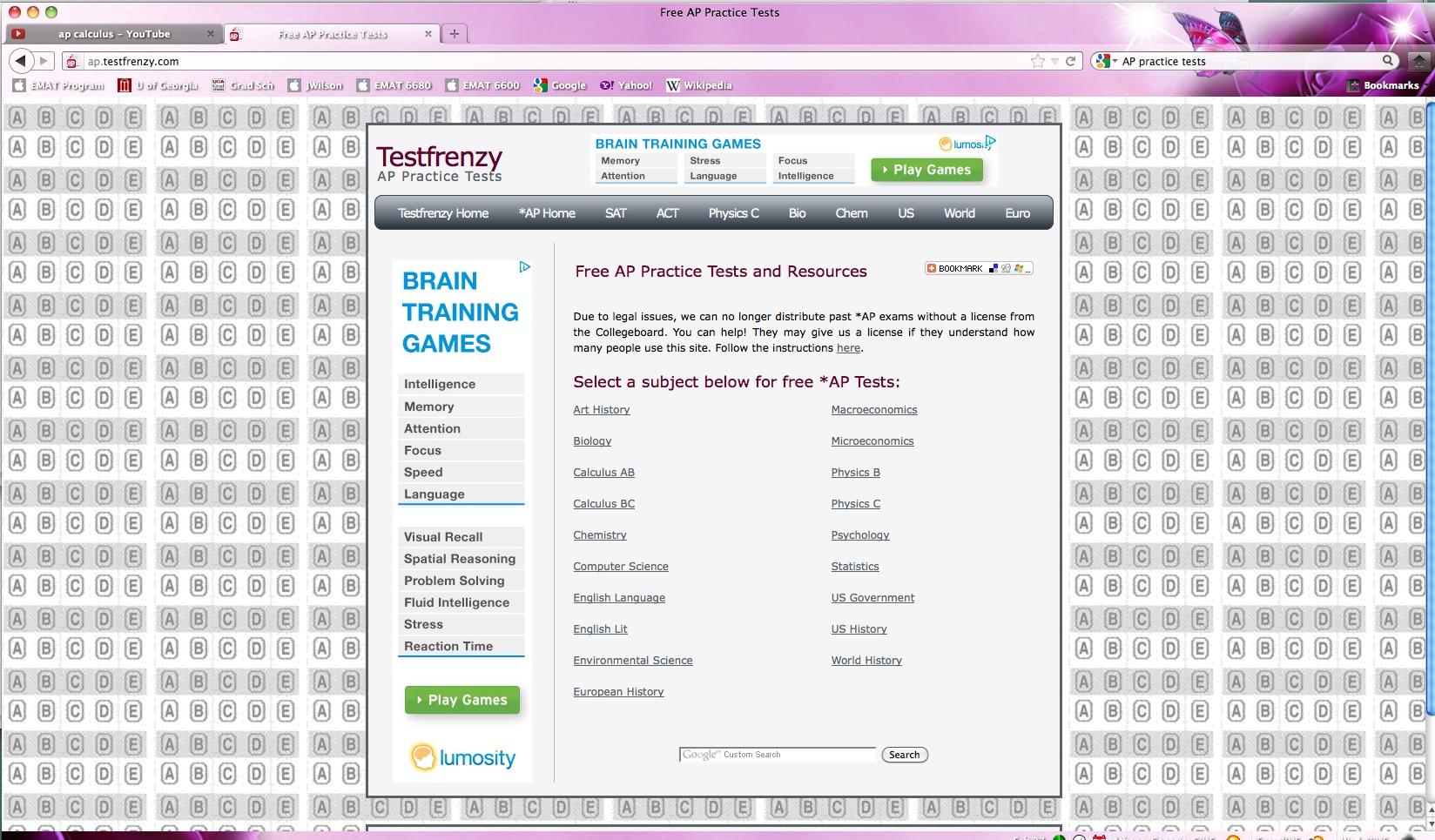
Of course you do notice the asterisk by the word free. Remember, these high stakes test are a big money maker. What will it actually cost? What you find is there are some broken links, but there are also some good links.
They have a connection to MIT which offers many of their courses including calculus open source over the internet. You pick the subtopic and it takes you right to a lecture video, a pdf of the notes or a link to a useful applet from another college or university.
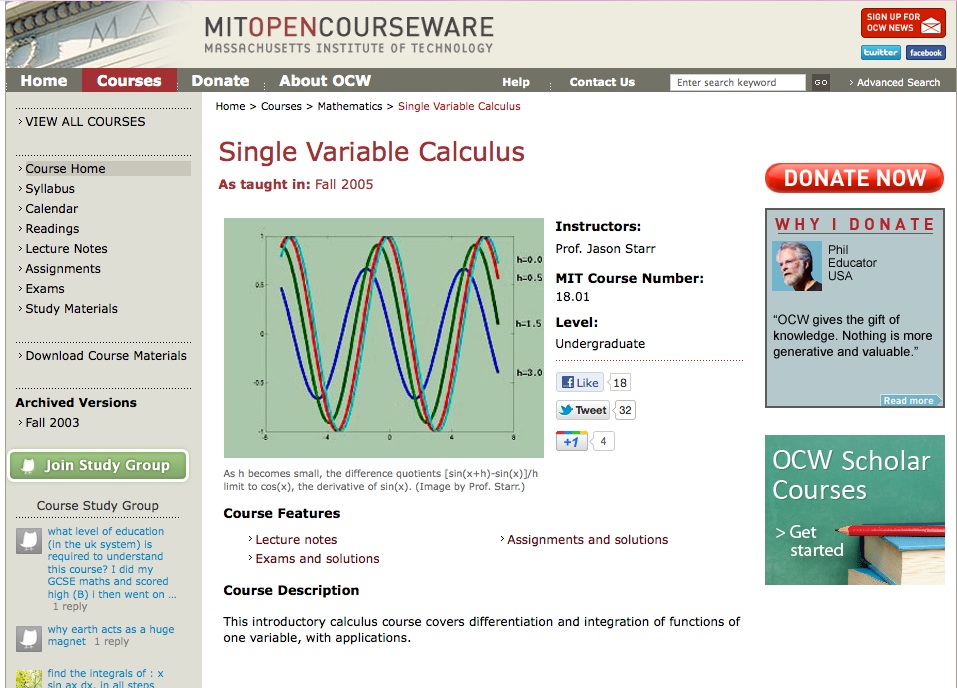
Here is an example of the type of video lecture a student may use on the MIT open course. There are extensive lectures for both single and multivariable calculus.You notice that there are exams with solutions, but are they the same type of questions that you will see on the AP? The College Board which is the parent company of the AP puts out a bulletin with practice questions of course.
Click here to view it.
Geometers sketchpad offers some useful conceptual knowledge for the exam. One conceptual under pining of the derivative is to think about the average rate of change between two points when the distance between them has become what Newton called, "the infinitesimal." This can be thought of as the instantaneous rate of change. This sketchpad document started with the graph of y equals x cubed. We put two points A and B as infinitely close to each other as we possible could and animated them to move together up the graph. We notice the the slope of line connecting our infinitely close points is remarkably close to the value of three times the x valued squared which can be shown to be our first derivative. This sketch was conceptualized by my classmate Doris Santorini. Click here for the sketch.
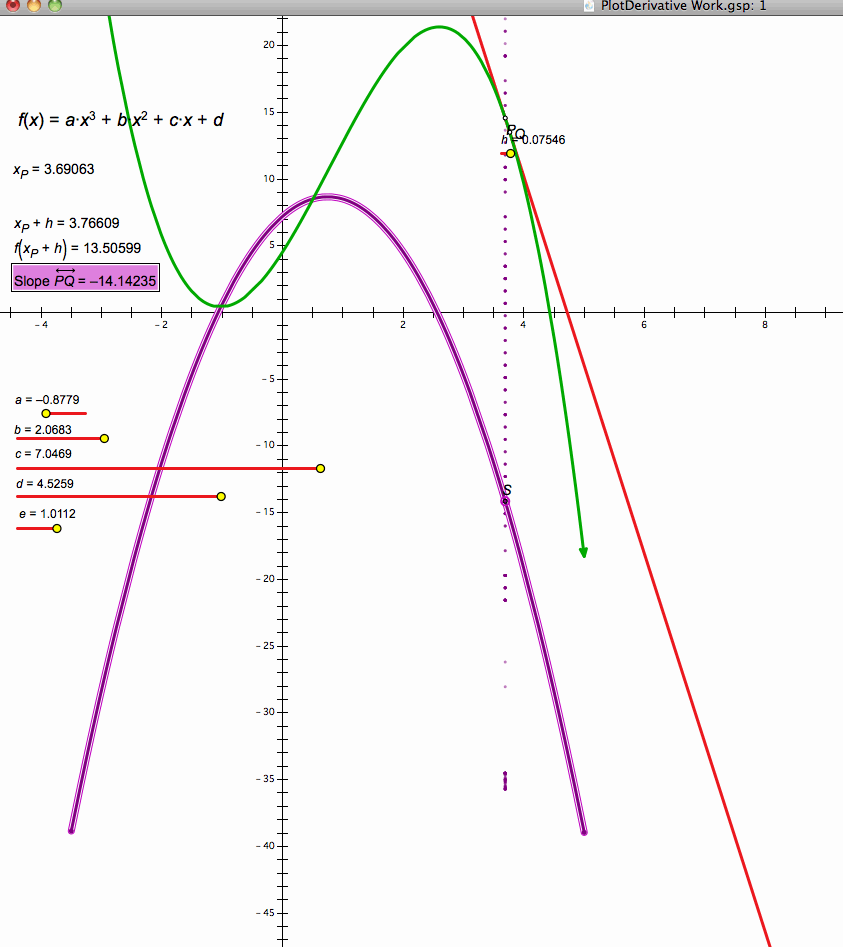
Geometers sketchpad offers many tools on its Learning Center that can help an AP calculus student or a teacher for that matter. This example is called Plotting the Derivative. Here is how the sketch approaches this limit: It is similar to the example just explained but with many more parameters that can be engaged. What I thought was real ingenious was the tracing of the derivative function by creating a point called S that had the x abscissa value of the cubic function and the slope of the infinitely close points as the ordinate y-value. The resultant locus or trace-however the student wants to do it is a graph of the first derivative equation. The sketch also allowed you to adjust the parameters of a, b. c, and d in a x cubed plus or minus b x squared plus or minus c x plus or minus d. Here is the student activity sheet, and the sketch:
Sketchpad has many activities that are available to students to aquire vital skills for the AP Calculus AB exam. Here is an example of of how sketchpad handles integration:
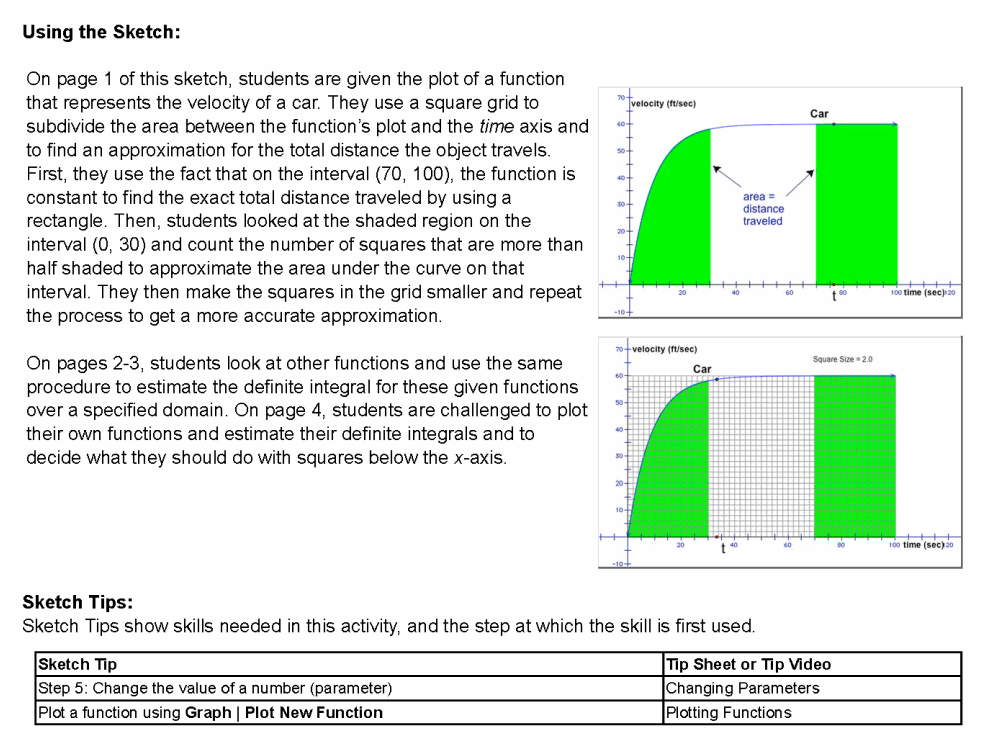
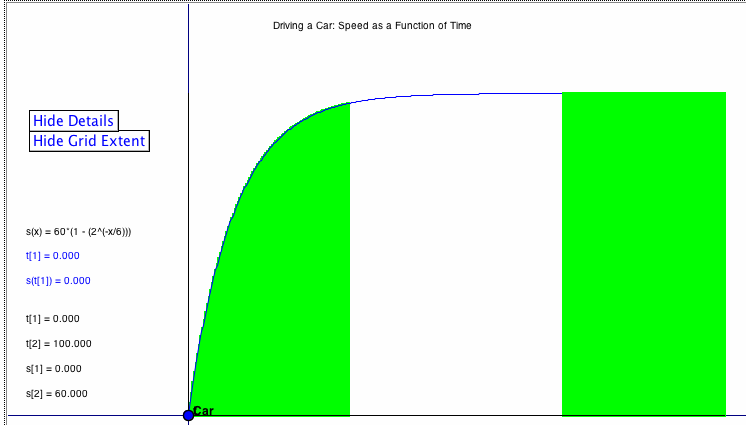
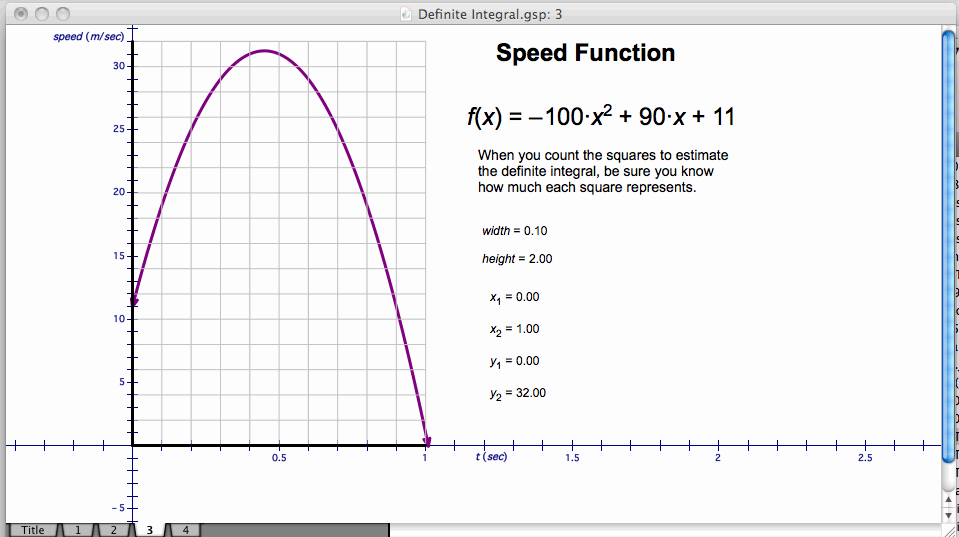what can I
Here is how sketchpad handles the instruction of the Taylor Series:
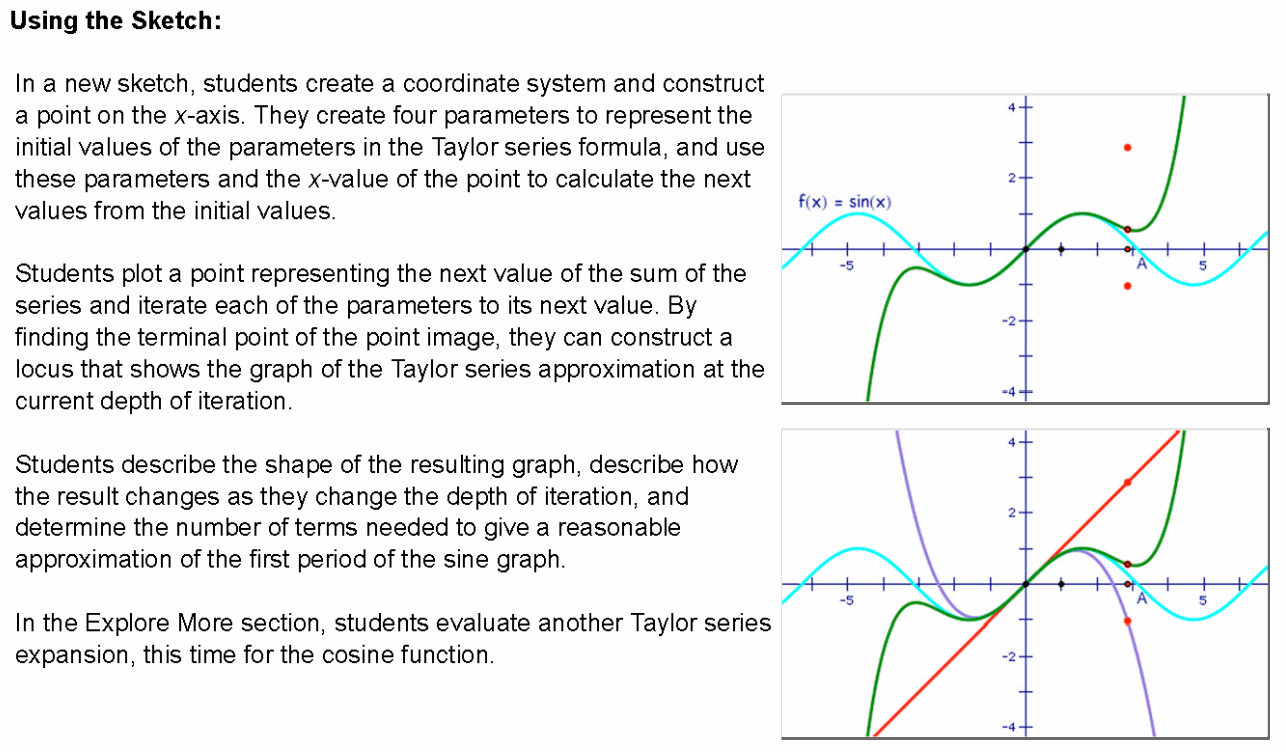
http://webspace.ship.edu/msrenault/GeoGebraCalculus/GeoGebraCalculusApplets.html These are sme great apps using geogebra to show calculus concepts.
The open response sectioins have great opportunity for slef-guided study with the aide of youtube by Google. There is a plethora of great videos showing past open response problems and their completey worked out swolution sets. Here is an example. Click the beside image to watch the video:
Calculus Video for free and open response
The Graphing Calculator program that comes as standard equipment on Apple Macintosh computers offers a great deal of functionality for students struggleing to grasp complex calculus topics.
Here is an example oft he aformentioned Taylor Series. The n value reflects the the number of terms that are present.
In summary, although there is no substitute for a knowledgeable instructor and a proper brick and mortar class meeting, there are many opportunities for calculus students to supplement and often times exceed their previous understanding of complex topics using sophisticated software and the communication properties of computers and technology. For example, what other time in history, could you hear and see a fanatastic lecture by a MIT scholar on rate of change problems when you are nowhere near the city of Boston? As I've shown, now you can. You can also access and take practice tests direct from the College Board to prepare for the proper performance. You can see complex topics like Taylor series and definite integrals under dynamic conditions and manipulate the variables that change the parameters of the equations. Although this essay just scrapes the tip of the iceberg, it is evident that we are in a golden age of technology for learning calculus