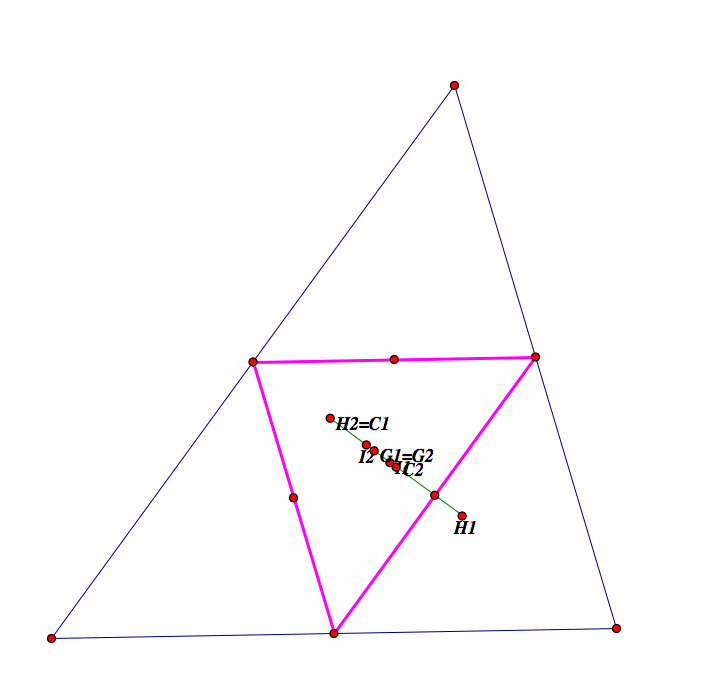By Alicia Rosenberger
Consider the rational equations of the form
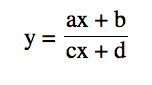
Explore the mathematical ideas for various values of the parameters a, b, c, and d. What can we say about this? First, we can say that this graph is a hyperbola. More specifically it is a rectangular hyperbola, therefore the asymptotes on the graph will be perpendicular to each other. Where the perpendicular asymptotes cross is the center of the hyperbola.
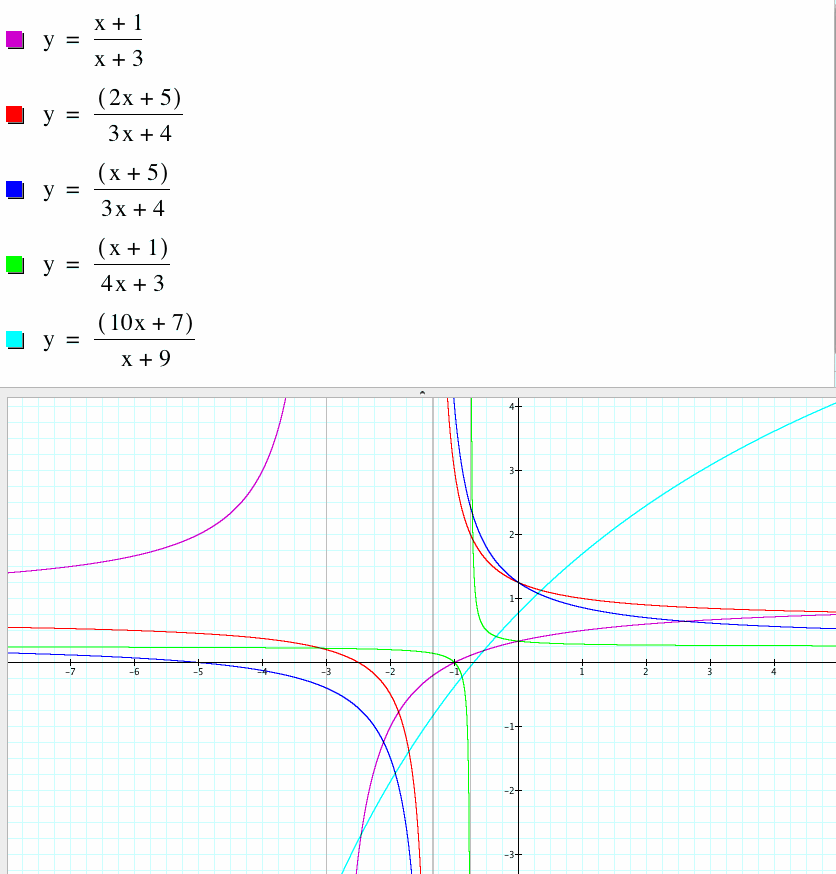
let's look more closely and let b=2, c=1, d=3, and vary the values of a:
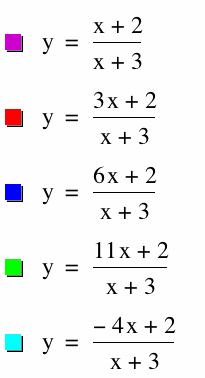
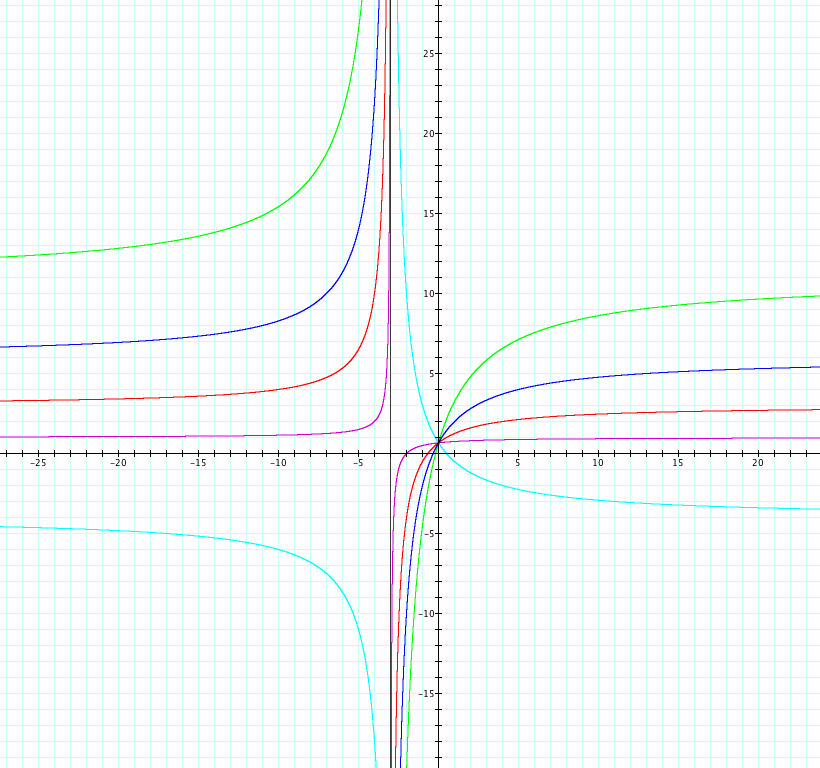
We start to notice that as a increases, the curves become less rigid, and so they become more round and the asymptotes become more spread out. We also see that when a is less than zero, the graph is reflected over the line x= -3, but the asymptote stays in the same place at x= -3 because that is where the denominator of our equation is undefined since we have fixed d at a value of 3.
If we fix a=1, c=2, d=3, and vary b:
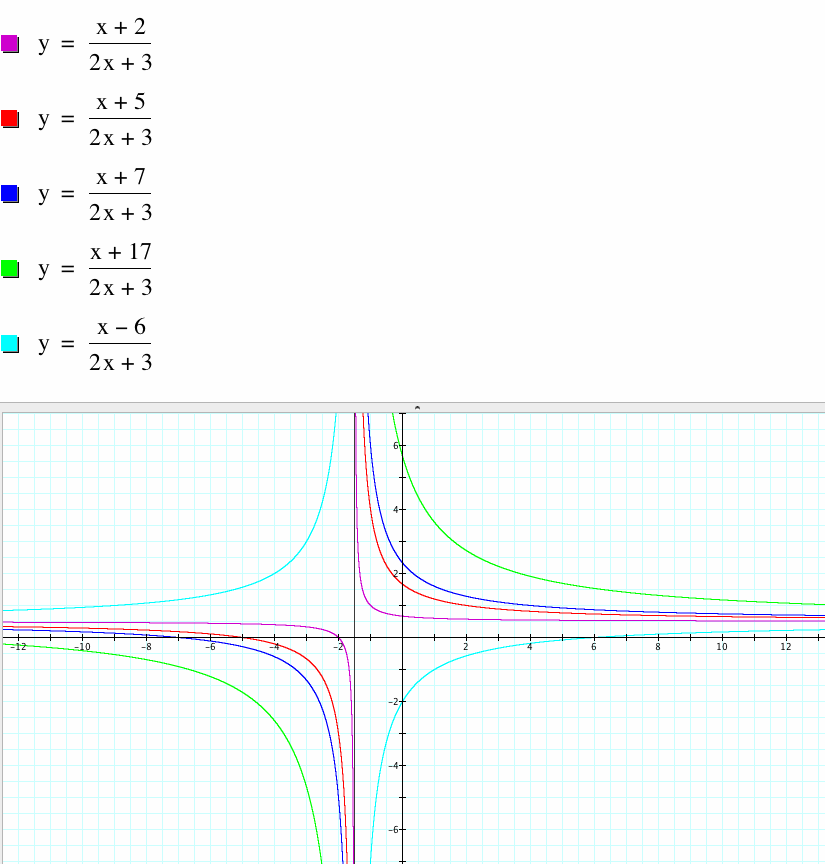
Notice that these equations are undefinded when x= -1.5, which is where we have a vertical asymptote. We also notice that as b increases, the graph becomes more round, less rigid, and wider (shifting horizontally and vertically), similar to what we saw before when varying a, except the graph is reflected over the line x= -1.5 when we vary b. But the graph looks like the previous one when b is negative, it is reflected.
Now, let's fix a=1, b=2, d=3 and vary c:
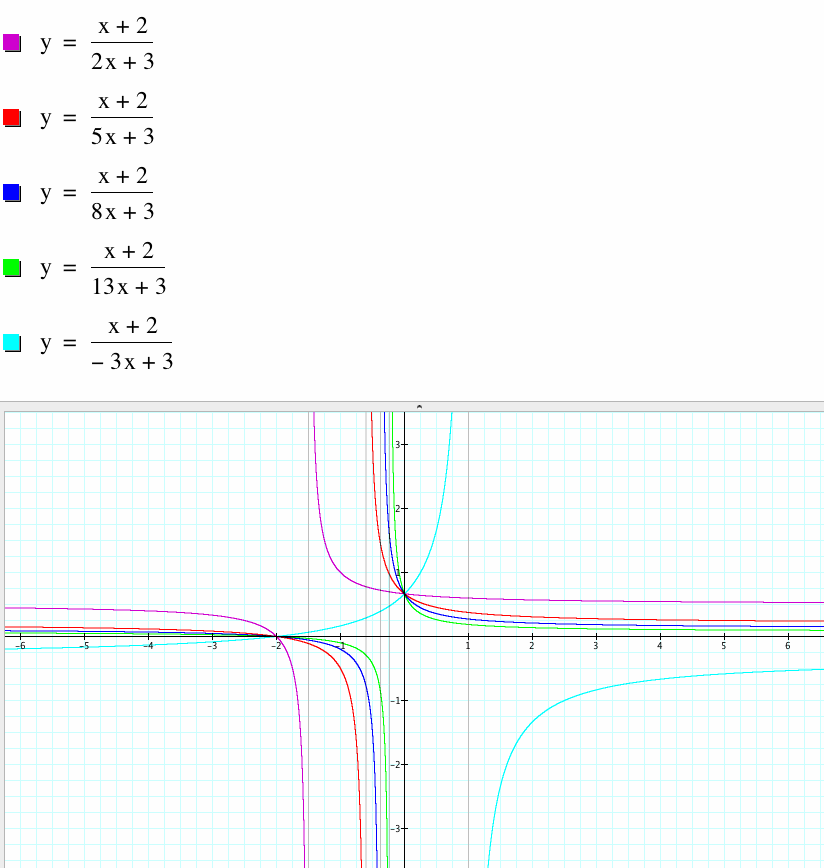
Here we have something similar to when we fixed a,c,d and varied b. Except, instead of the graph moving out, this time the graph is shifting vertically instead of horizontally and vertically. We see many vertical asymptotes because we are varying the value of c, so the denominator will be undefined at different values of x depending on the equation or given value of c for that equation. When c is negative, we see that the graph is reflecetd over the line x= -1/3, as we have seen in the previous two examples.
Let's look at what happens when we fix a=1, b=2, c=3, and vary d:
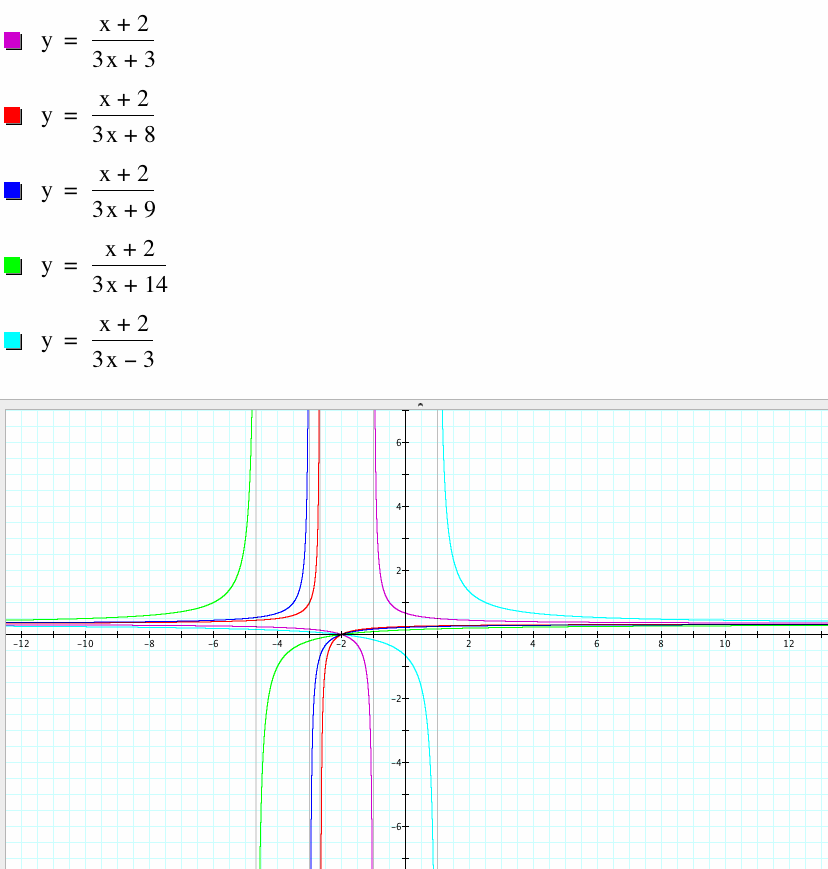
We see here that the vertical asymptotes will also vary because the denominator will be undefined depending on the value of d. We also notice the difference between the pink graph and the red one and why they have reflected over the line x= -2 when there is no sign change...the red and blue graph are similar, the blue is shifted slightly vertically and horizontally with the increase of d from 8 to 9. The green graph has shifted vertically by changing d. When d is negative, we see the pattern where the graph is reflected.
square inscribed in a semicircle:
Given a semicircle with an inscribed square of side s.
Let a be the length on the diameter on each side of the square
Find ![]()
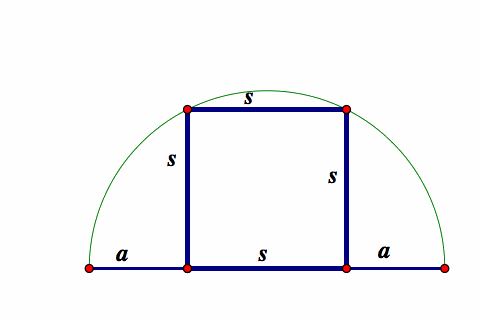
now we want to find ![]()
In order to do this:

Take any triangle. Construct a triangle connecting the three midpoints of the sides. This is called the MEDIAL triangle. It is similar to the original triangle and one-fourth of its area. Construct G, H, C, and I for this new triangle. Compare to G, H, C, and I in the original triangle.
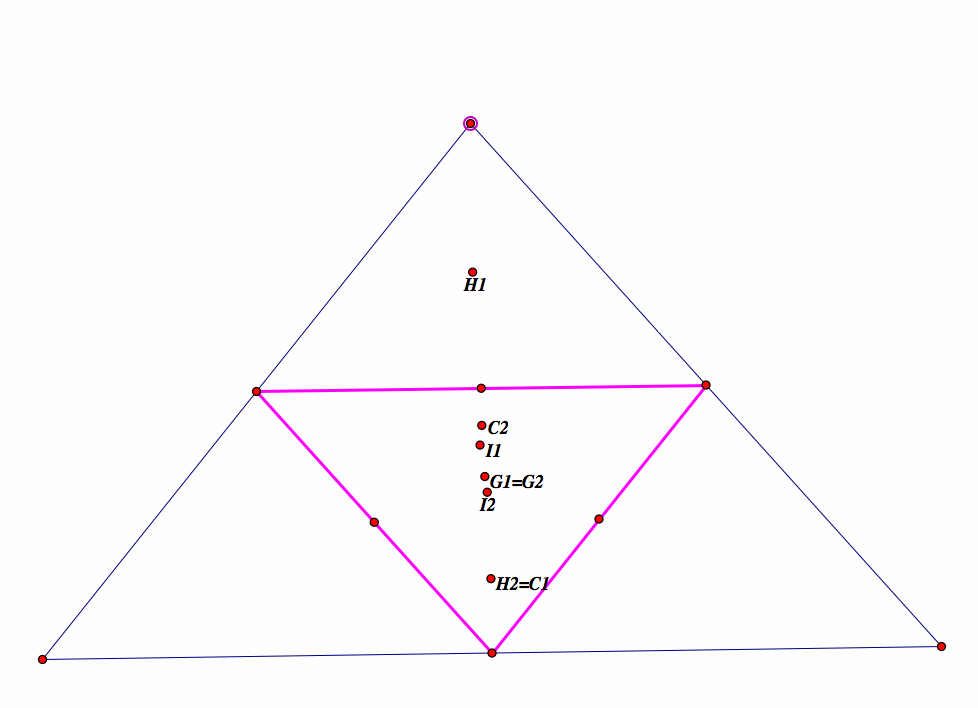
If we compare the medial triangle to the original triangle (blue), we see a few things:
first, let G1,H1,C1,I1 be the centroid, orthocenter, circumcenter, and incenter for the original blue triangle, respectively.
Let, G2,H2,C2,I2 be the centroid, orthocenter, circumcenter, and incenter for the medial pink triangle, respectively.
We notice that the centroid is the same for both triangles
The orthocenters are on opposite ends. They do not meet
The circumcenters do not meet either, however, the circumcenter for the first triangle is where the orthocenter for the medial triangle is.
the incenters for the triangles are similar.
If we move the vertices of the original triangle, we start to see some interesting things:
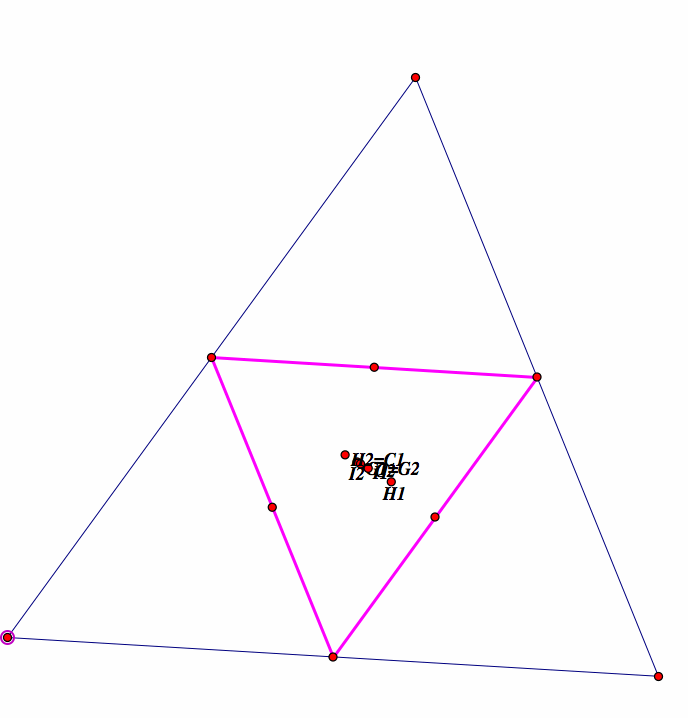
The centroid, orthocenter, circumcenter, and incenter of both triangles start to move together towards each other. However, they will never all be the same. It looks like they can be colinear, maybe not all of them, but we can manipulate the vertices of the triangle to make them lie in a line.