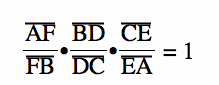---

---

Concurrency of Medians:

By Alicia Rosenberger

The CENTROID (G) of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side.

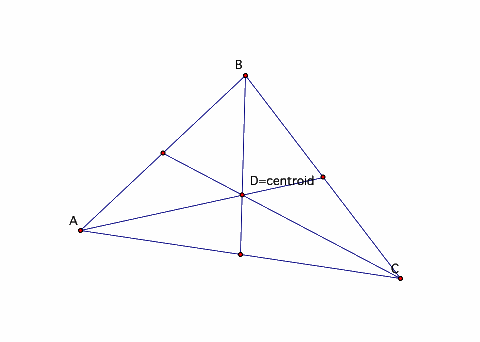
Show that the concurrency of the medians is a special case of Ceva's Theorem:

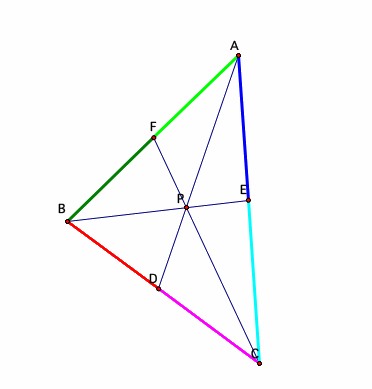
In the triangle ABC, the three medians AD, BE, and CF intersect at a single point P if and only if:

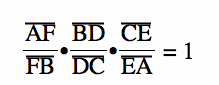
or in other words, using the GSP sketch above, if and only if:

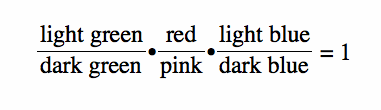
We can use Ceva's heorem to prove that if the Cevians are concurrent, meaning that the three medians intersect at one point P, then the ratio of the products is equal to 1.

Since the medians divide each of the sides of the triangle in half, it follows that AF=FB=1/2

BD=DC=1/2

CE=EA=1/2

Thus,

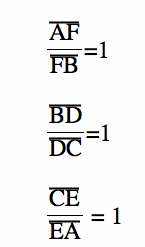
And the product of these three ratios is equal to 1: