By Alicia Rosenberger
Find all conditions in which the three vertices of the Pedal triangle are colinear (that is, it is a degenerate triangle). This line is called the Simson Line.
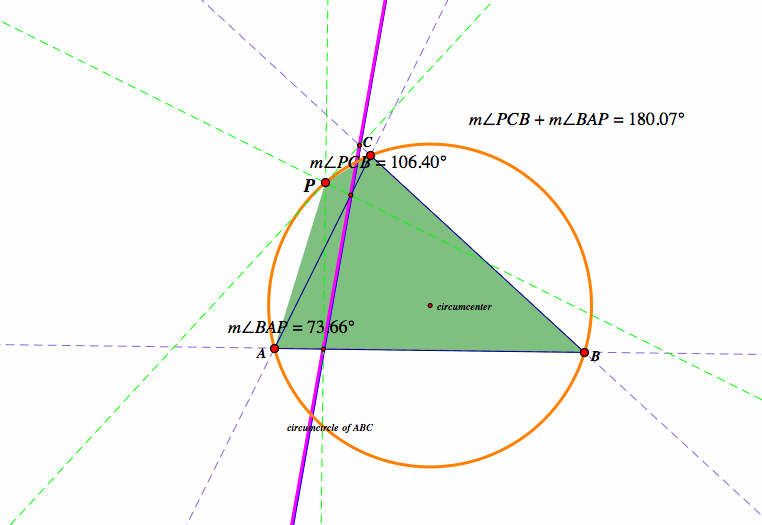
Let's start with a triangle ABC. If we let P be any point inside the triangle ABC, we can construct the Pedal Triangle by constructing perpendiculars from P to each of the sides of triangle ABC. The points where the perpendiculars intersect the original triangle ABC, are the vertices of the Pedal Triangle.
The Simson Line can be found when we have the circumcircle of triangle ABC. We can extend the segments of triangle ABC to see more clearly. If we drop a perpendicular from point P inside the triangle to each of the extended lines that make up the sides of triangle ABC, the intersection point of the perpendicular with these lines forms three points. These three points, when they lie on the same line (collinear), they form a line called the Simson Line. These three points happen to be the vertices of the Pedal Triangle. So when the vertices of the Pedal Triangle are colinear, we have a degenerate triangle, or the Simson Line now.
But when does this happen?
when P is inside triangle ABC, the Pedal Triangle is also contained inside triangle ABC:
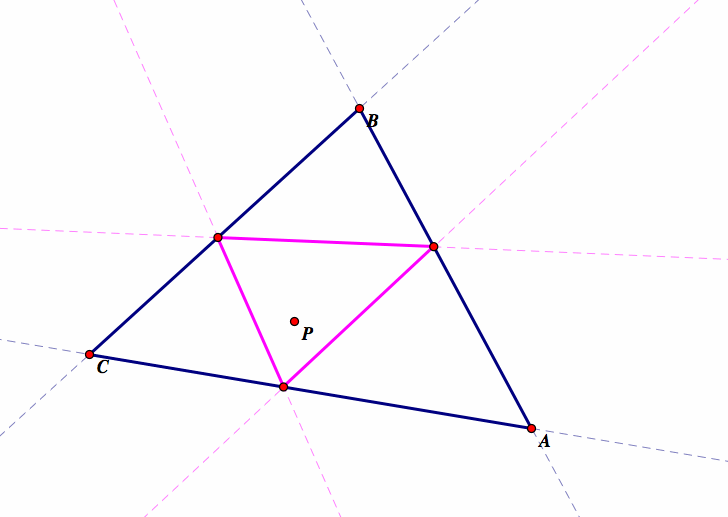
As we move P towards the vertices of triangle ABC, we see the Pedal Triangle starting to collapse because two of the angles of the Pedal Triangle are decreasing as we move P, while the third angle is approaching 180 degrees. As this happens, the altitude of the Pedal Triangle is approaching zero and the vertex of the altitude of the triangle is moving towards the base of the triangle:
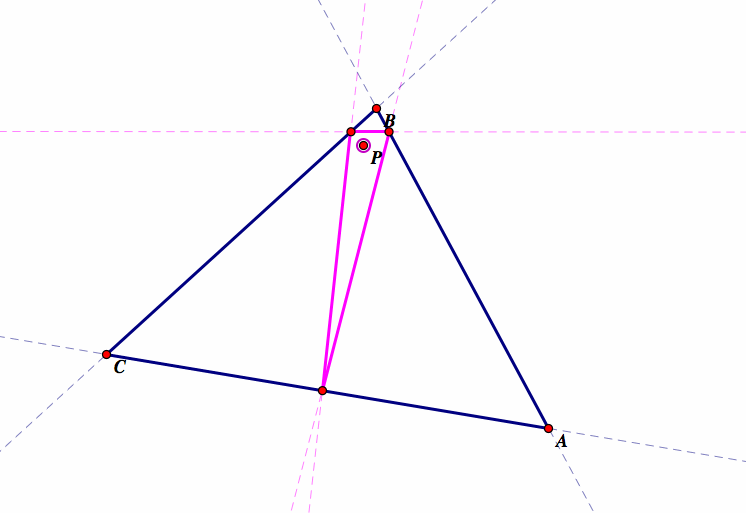
So we see that if we place point P on one of the vertices of the original triangle from which the Pedal Triangle was constructed (ABC), the Pedal Triangle becomes degenerate, where the vertices of the Pedal Triangle are colinear, two of the angles of the Pedal Triangle are 0 degrees, and one of the angles is 180 degrees. We also see now that the altitude of the Pedal Triangle has become zero because the triangle has collapsed. This is the case because the Pedal Triangle is constructed by connecting the perpendicular inersections to the extended sides of the original triangle ABC. So if the pedal point P is coincident with any vertex of the original triangle ABC, then the perpendicular to those sides of the triangle has length zero. Therefore, the resulting triangle degenerates. We can see that when this is the case, we have created the Simson Line, where the vertices of the Pedal Triangle are colinear, which is the same as saying that the feet of the perpendiculars from P are all colinear. Notice also, that the Simson Line becomes the altitude of the original triangle ABC.
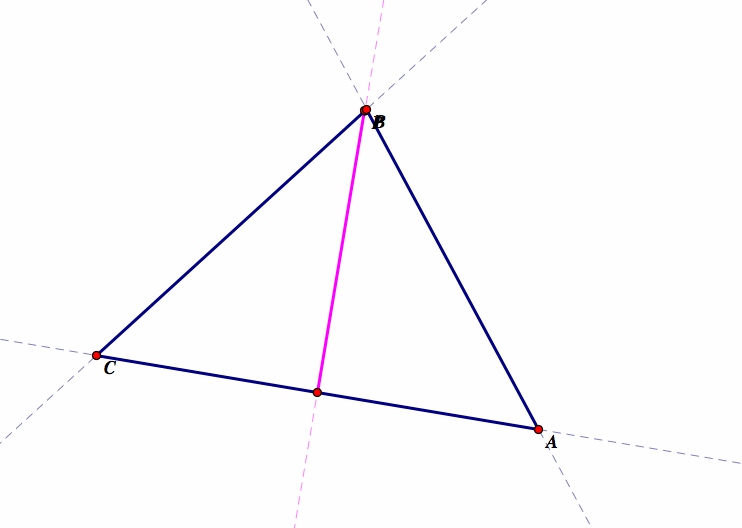
If we were to trace point P where the Pedal Triangle is degenerate, we would see that it is degenerate along the circumcircle of triangle ABC (third figure below). This lies in the definition of the Simson Line, that it is formed by the perpendiculars from a point P that is on the circumcircle of the triangle.
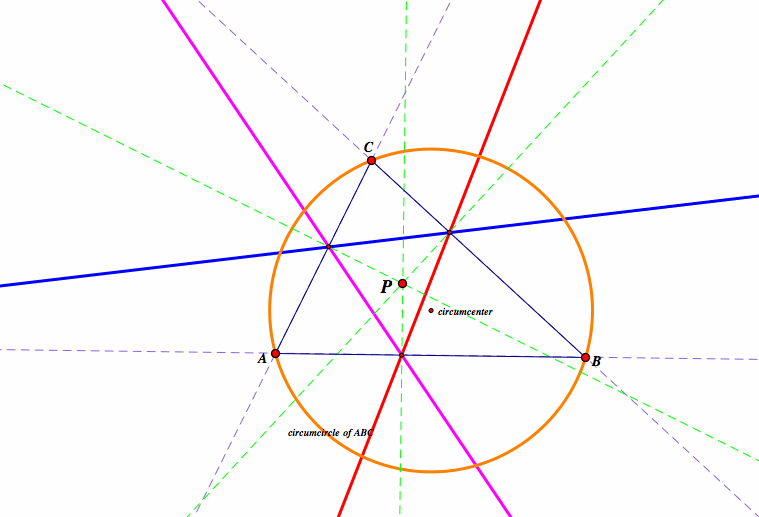
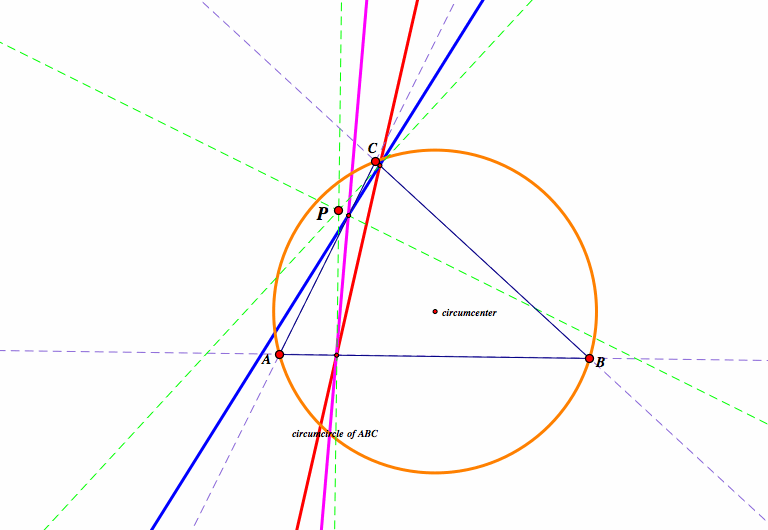
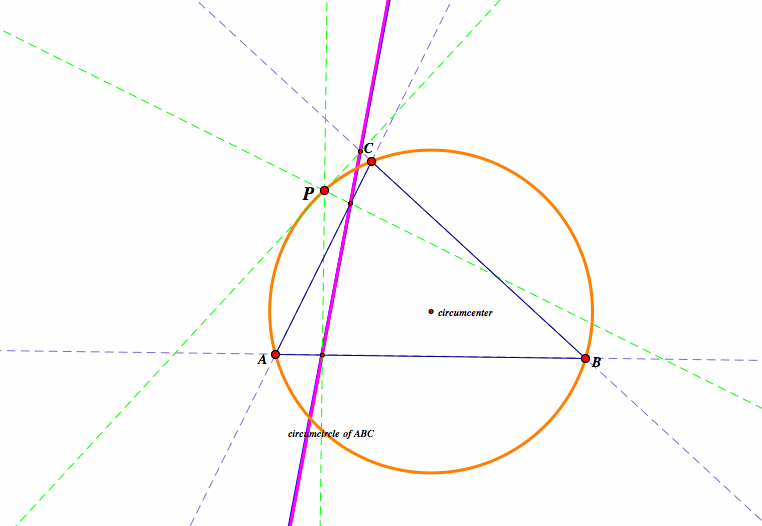
The feet of the perpendiculars to each of the sides form a point P which must be on the circumcircle in order to form the Simson Line because if we were to construct a quadrilateral with the three vertices of the triangle ABC and point P, we would see that when P lies on the circumcircle, the two opposite angles of the quadrilateral add up to 180 degrees.